
【题目】已知: ![]() 、
、 ![]() 、
、 ![]() 是同一平面上的三个向量,其中
是同一平面上的三个向量,其中 ![]() =(1,2).
=(1,2).
(1)若| ![]() |=2
|=2 ![]() ,且
,且 ![]() ∥
∥ ![]() ,求
,求 ![]() 的坐标.
的坐标.
(2)若| ![]() |=
|= ![]() ,且
,且 ![]() +2
+2 ![]() 与2
与2 ![]() ﹣
﹣ ![]() 垂直,求
垂直,求 ![]() 与
与 ![]() 的夹角θ
的夹角θ
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中, 曲线
中, 曲线![]() 的参数方程为
的参数方程为![]() 为参数) ;在以原点
为参数) ;在以原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中, 曲线
轴的正半轴为极轴的极坐标系中, 曲线![]() 的极坐标参数方程为
的极坐标参数方程为![]() .
.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若射线![]() 与曲线
与曲线![]() ,
,![]() 的交点分别为
的交点分别为![]() (
(![]() 异于原点). 当斜率
异于原点). 当斜率![]() 时, 求
时, 求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C方程为 ![]() (a>b>0),左、右焦点分别是F1 , F2 , 若椭圆C上的点P(1,
(a>b>0),左、右焦点分别是F1 , F2 , 若椭圆C上的点P(1, ![]() )到F1 , F2的距离和等于4. (Ⅰ)写出椭圆C的方程和焦点坐标;
)到F1 , F2的距离和等于4. (Ⅰ)写出椭圆C的方程和焦点坐标;
(Ⅱ)设点Q是椭圆C的动点,求线段F1Q中点T的轨迹方程;
(Ⅲ)直线l过定点M(0,2),且与椭圆C交于不同的两点A,B,若∠AOB为锐角(O为坐标原点),求直线l的斜率k0的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知方程x2+y2﹣2x﹣4y+m=0.
(1)若此方程表示圆,求m的取值范围;
(2)若(1)中的圆与直线x+2y﹣4=0相交于M、N两点,且OM⊥ON(O为坐标原点),求m;
(3)在(2)的条件下,求以MN为直径的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在![]() 中,
中, ![]() 的中点为
的中点为![]() ,且
,且![]() ,点
,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .固定边
.固定边![]() ,在平面内移动顶点
,在平面内移动顶点![]() ,使得圆
,使得圆![]() 与边
与边![]() ,边
,边![]() 的延长线相切,并始终与
的延长线相切,并始终与![]() 的延长线相切于点
的延长线相切于点![]() ,记顶点
,记顶点![]() 的轨迹为曲线
的轨迹为曲线![]() .以
.以![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 为坐标原点如图所示建立平面直角坐标系.
为坐标原点如图所示建立平面直角坐标系.
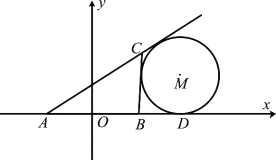
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)设动直线![]() 交曲线
交曲线![]() 于
于![]() 两点,且以
两点,且以![]() 为直径的圆经过点
为直径的圆经过点![]() ,求
,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在(﹣∞,0)∪(0,+∞)上的函数f(x),如果对于任意给定的等比数列{an},{f(an)}仍是等比数列,则称f(x)为“保等比数列函数”.现有定义在(﹣∞,0)∪(0,+∞)上的如下函数:①f(x)=x2;②f(x)=2x;③f(x)= ![]() ;④f(x)=ln|x|.则其中是“保等比数列函数”的f(x)的序号为( )
;④f(x)=ln|x|.则其中是“保等比数列函数”的f(x)的序号为( )
A.①②
B.③④
C.①③
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() ,半径为
,半径为![]() 的圆
的圆![]() 与
与![]() 相切,圆心
相切,圆心![]() 在
在![]() 轴上且在直线
轴上且在直线![]() 的上方.
的上方.
(Ⅰ)求圆![]() 的标准方程;
的标准方程;
(Ⅱ)过点![]() 的直线与圆
的直线与圆![]() 交于
交于![]() 两点(
两点(![]() 在
在![]() 轴上方),问在
轴上方),问在![]() 轴正半轴上是否存在点
轴正半轴上是否存在点![]() ,使得
,使得![]() 轴平分
轴平分![]() ?若存在,请求出点
?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列函数中,在其定义域内既是奇函数又是减函数的是( )
·(1)y=﹣|x|(x∈R)(2)y=﹣x3﹣x(x∈R)(3)y=( ![]() )x(x∈R)(4)y=﹣x+
)x(x∈R)(4)y=﹣x+ ![]() .
.
A.(2)
B.(1)(3)
C.(4)
D.(2)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小王创建了一个由他和甲、乙、丙共4人组成的微信群,并向该群发红包,每次发红包的个数为1个(小王自己不抢),假设甲、乙、丙3人每次抢得红包的概率相同.
(Ⅰ)若小王发2次红包,求甲恰有1次抢得红包的概率;
(Ⅱ)若小王发3次红包,其中第1,2次,每次发5元的红包,第3次发10元的红包,记乙抢得所有红包的钱数之和为X,求X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com