
【题目】如图,半圆![]() 的直径为
的直径为![]() ,
, ![]() 为直径延长线上的一点,
为直径延长线上的一点, ![]() ,
, ![]() 为半圆上任意一点,以
为半圆上任意一点,以![]() 为一边作等边三角形
为一边作等边三角形![]() ,设
,设![]()
![]() .
.
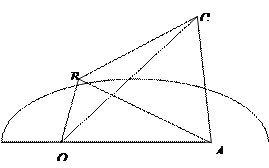
(1)当![]() 为何值时,四边形
为何值时,四边形![]() 面积最大,最大值为多少;
面积最大,最大值为多少;
(2)当![]() 为何值时,
为何值时, ![]() 长最大,最大值为多少.
长最大,最大值为多少.
科目:高中数学 来源: 题型:
【题目】已知△ABC中,角A、B、C的对边分别为a、b、c,已知a=2,A=45°,若三角形有两解,则边b的取值范围是( )
A.b>2
B.b<2
C.2<b<2 ![]()
D.2<b<2 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】36的所有正约数之和可按如下方法得到:因为36=22×32 , 所以36的所有正约数之和为(1+3+32)+(2+2×3+2×32)+(22+22×3+22×32)=(1+2+22)(1+3+32)=91,参照上述方法,可得100的所有正约数之和为( )
A.217
B.273
C.455
D.651
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2 ![]() sin(
sin( ![]() ωx)cos(
ωx)cos( ![]() ωx)+2cos2(
ωx)+2cos2( ![]() ωx)(ω>0),且函数f(x)的最小正周期为π.
ωx)(ω>0),且函数f(x)的最小正周期为π.
(1)求ω的值;
(2)求f(x)在区间 ![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=2ln(x+2)﹣(x+1)2 , g(x)=k(x+1).
(1)求f(x)的单调区间;
(2)当k=2时,求证:对于x>﹣1,f(x)<g(x)恒成立;
(3)若存在x0>﹣1,使得当x∈(﹣1,x0)时,恒有f(x)>g(x)成立,试求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是公差不为零的等差数列,满足
是公差不为零的等差数列,满足![]() 数列
数列![]() 的通项公式为
的通项公式为![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)将数列![]() ,
,![]() 中的公共项按从小到大的顺序构成数列
中的公共项按从小到大的顺序构成数列![]() ,请直接写出数列
,请直接写出数列![]() 的通项公式;
的通项公式;
(3)记![]() ,是否存在正整数
,是否存在正整数![]()
![]() ,使得
,使得![]() 成等差数列?若存在,求出
成等差数列?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四边形![]() 是正方形,
是正方形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 都是等边三角形,
都是等边三角形, ![]() 、
、![]() 、
、![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 、
、![]() 、
、![]() 的中点,分别以
的中点,分别以![]() 、
、![]() 、
、![]() 、
、![]() 为折痕将四个等边三角形折起,使得
为折痕将四个等边三角形折起,使得![]() 、
、![]() 、
、![]() 、
、![]() 四点重合于一点
四点重合于一点![]() ,得到一个四棱锥.对于下面四个结论:
,得到一个四棱锥.对于下面四个结论:
①![]() 与
与![]() 为异面直线; ②直线
为异面直线; ②直线![]() 与直线
与直线![]() 所成的角为
所成的角为![]()
③![]() 平面
平面![]() ; ④平面
; ④平面![]() 平面
平面![]() ;
;
其中正确结论的个数有( )

A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,
, ![]() (
( ![]() 为自然对数的底数).
为自然对数的底数).
(1)设曲线 ![]() 在
在 ![]() 处的切线为
处的切线为 ![]() ,若
,若 ![]() 与点
与点 ![]() 的距离为
的距离为 ![]() ,求
,求 ![]() 的值;
的值;
(2)若对于任意实数 ![]() ,
, ![]() 恒成立,试确定
恒成立,试确定 ![]() 的取值范围;
的取值范围;
(3)当 ![]() 时,函数
时,函数 ![]() 在
在 ![]() 上是否存在极值?若存在,请求出极值;若不存在,请说明理由.
上是否存在极值?若存在,请求出极值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系xoy中,直线l的参数方程为 ![]() (t为参数,
(t为参数, ![]() ),以坐标原点o为极点,x轴的正半轴为极轴,并取相同的长度单位,建立极坐标系.曲线
),以坐标原点o为极点,x轴的正半轴为极轴,并取相同的长度单位,建立极坐标系.曲线 ![]()
(1)若直线l曲线 ![]() 相交于点
相交于点 ![]() ,
, ![]() ,
, ![]() ,证明:
,证明: ![]() 为定值;
为定值;
(2)将曲线 ![]() 上的任意点
上的任意点 ![]() 作伸缩变换
作伸缩变换 ![]() 后,得到曲线
后,得到曲线 ![]() 上的点
上的点 ![]() ,求曲线
,求曲线 ![]() 的内接矩形
的内接矩形 ![]() 周长的最大值.
周长的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com