
【题目】已知数列{an}满足an+1=an﹣2anan+1 , an≠0且a1=1.
(1)求数列{an}的通项公式;
(2)令 ![]() ,求数列{bn}的前2n项和T2n .
,求数列{bn}的前2n项和T2n .
【答案】
(1)证明:∵an+1=an﹣2an+1an,an≠0且a1=1,
∴ ![]() ﹣
﹣ ![]() =2,
=2,
∴数列{ ![]() }是等差数列,首项为1,等差数列为2.
}是等差数列,首项为1,等差数列为2.
∴ ![]() =1+2(n﹣1)=2n﹣1,
=1+2(n﹣1)=2n﹣1,
解得an= ![]()
(2)解: ![]() =(﹣1)n+1
=(﹣1)n+1 ![]()
=(﹣1)n+1 ![]() (
( ![]() +
+ ![]() ),
),
∴T2n= ![]() [(1+
[(1+ ![]() )﹣(
)﹣( ![]() +
+ ![]() )+…+(
)+…+( ![]() +
+ ![]() )﹣(
)﹣( ![]() +
+ ![]() )]
)]
= ![]() (1﹣
(1﹣ ![]() )=
)= ![]()
【解析】(1)由an+1=an﹣2an+1an , an≠0且a1=1,取倒数可得 ![]() ﹣
﹣ ![]() =2,运用等差数列的通项公式即可得出.(2)
=2,运用等差数列的通项公式即可得出.(2) ![]() =(﹣1)n+1
=(﹣1)n+1 ![]() =(﹣1)n+1
=(﹣1)n+1 ![]() (
( ![]() +
+ ![]() ),利用“裂项求和”即可得出.
),利用“裂项求和”即可得出.
【考点精析】通过灵活运用数列的前n项和和数列的通项公式,掌握数列{an}的前n项和sn与通项an的关系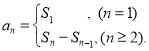 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 首项为a1且1,an , Sn成等差数列.
(1)求数列{an}的通项公式;
(2)数列{bn}满足bn=(log2a2n+1)×(log2a2n+3),求数列 ![]() 的前n项和Tn .
的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)满足下列条件:在定义域内存在x0 , 使得f(x0+1)=f(x0)+f(1)成立,则称函数f(x)具有性质M;反之,若x0不存在,则称函数f(x)不具有性质M.
(1)证明:函数f(x)=2x具有性质M,并求出对应的x0的值;
(2)已知函数 ![]() 具有性质M,求a的取值范围.
具有性质M,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位同学期末考试的语文、数学、英语、物理成绩如茎叶图所示,其中甲的一个数据记录模糊,无法辨认,用a来表示,已知两位同学期末考试四科的总分恰好相同,则甲同学四科成绩的中位数为( )
A.92
B.92.5
C.93
D.93.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解全校高中学生五一小长假参加实践活动的情况,抽查了100名学生,统计他们假期参加实践活动的时间,绘成的频率分布直方图如图所示.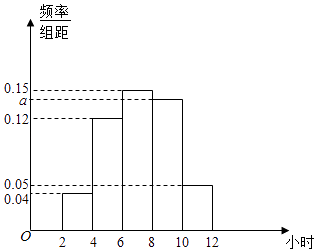
(1)求这100名学生中参加实践活动时间在6~10小时内的人数;
(2)估计这100名学生参加实践活动时间的众数、中位数和平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex(x2+x+a)在(0,f(0))处的切线与直线2x﹣y﹣3=0平行,其中a∈R.
(1)求a的值;
(2)求函数f(x)在区间[﹣2,2]上的最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,a,b,c分别是三个内角A,B,C的对边,若2asinB= ![]() b. (Ⅰ)求A;
b. (Ⅰ)求A;
(Ⅱ)若a= ![]() ,△ABC的面积为
,△ABC的面积为 ![]() ,求△ABC的周长.
,求△ABC的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com