
分析 (1)由三角函数公式化简可得f(x)=$\sqrt{2}sin({2x+\frac{π}{4}})+1$,由周期公式可得,解不等式-$\frac{π}{2}$+2kπ≤2x+$\frac{π}{4}$≤$\frac{π}{2}$+2kπ可得单调增区间;
(2)解$2x+\frac{π}{4}=kπ$,可得f(x)的图象的对称中心,解$2x+\frac{π}{4}=\frac{π}{2}+kπ$可得对称轴方程.
解答 解:(1)由三角函数公式化简可得f(x)=1+2sinxcosx+cos2x
=1+sin2x+cos2x=$\sqrt{2}sin({2x+\frac{π}{4}})+1$,
∴函数f(x)的最小正周期为T=$\frac{2π}{2}$=π,
由-$\frac{π}{2}$+2kπ≤2x+$\frac{π}{4}$≤$\frac{π}{2}$+2kπ可得$-\frac{3π}{8}+kπ≤x≤\frac{π}{8}+kπ,\;\;({k∈Z})$,
∴f(x)的单调增区间是$[{-\frac{3π}{8}+kπ,\;\;\frac{π}{8}+kπ}]$,k∈Z;
(2)令$2x+\frac{π}{4}=kπ$,则$x=-\frac{π}{8}+\frac{kπ}{2},k∈Z$,
∴f(x)的图象的对称中心为(-$\frac{π}{8}$+$\frac{kπ}{2}$,1),k∈Z,
令$2x+\frac{π}{4}=\frac{π}{2}+kπ$,得x=$\frac{π}{8}$+$\frac{kπ}{2}$,k∈Z,
∴f(x)的图象的对称轴方程为x=$\frac{π}{8}$+$\frac{kπ}{2}$,k∈Z
点评 本题考查三角函数的单调性和对称性,属基础题.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
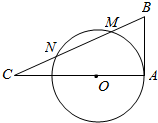 如图所示,已知AD为⊙O的直径,AB为⊙O的切线,割线BN的延长线交AD的延长线于点C,且BM=MN=NC,若AB=2,则该圆的直径AD的长为$\frac{5}{7}\sqrt{14}$.
如图所示,已知AD为⊙O的直径,AB为⊙O的切线,割线BN的延长线交AD的延长线于点C,且BM=MN=NC,若AB=2,则该圆的直径AD的长为$\frac{5}{7}\sqrt{14}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com