
【题目】设命题p:m∈{x|x2+(a﹣8)x﹣8a≤0},命题q:方程 ![]() =1表示焦点在x轴上的双曲线.
=1表示焦点在x轴上的双曲线.
(1)若当a=1时,命题p∧q假命题,p∨q”为真命题,求实数m的取值范围;
(2)若命题p是命题q的充分不必要条件,求实数a的取值范围.
【答案】
(1)解:a=1时,x2+(a﹣8)x﹣8a≤0,
即x2﹣7x﹣8≤0,解得:﹣1≤x≤8,
故p:﹣1≤m≤8,
若方程 ![]() =1表示焦点在x轴上的双曲线,
=1表示焦点在x轴上的双曲线,
则 ![]() ,解得:m>5
,解得:m>5
故q:m>5;
若命题p∧q假命题,p∨q”为真命题,
则p,q一真一假,
故 ![]() 或
或 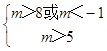 ,
,
解得:m∈[﹣1,5]∪(8,+∞)
(2)解:命题p:m∈{x|x2+(a﹣8)x﹣8a≤0}={x|(x﹣8)(x+a)≤0},
﹣a<8即a>﹣8时,p:[﹣a,8],
﹣a>8,即a<﹣8时,p:[8,﹣a],
q:m>5,
若命题p是命题q的充分不必要条件,
即[﹣a,8](5,+∞),或[8,﹣a](5,+∞),
故﹣a>5,解得:a<﹣5
【解析】(1)分别求出p,q为真时的m的范围,根据p,q一真一假,得到关于m的不等式组,解出即可;(2)通过讨论a的范围,得到关于m的不等式组,解出即可.
【考点精析】掌握复合命题的真假是解答本题的根本,需要知道“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反;“p且q”形式复合命题当P与q同为真时为真,其他情况时为假;“p或q”形式复合命题当p与q同为假时为假,其他情况时为真.


科目:高中数学 来源: 题型:
【题目】已知等比数列{an}中,a1=64,公比q≠1,a2 , a3 , a4又分别是某个等差数列的第7项,第3项,第1项.
(1)求an;
(2)设bn=log2an , 求数列{|bn|}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在单调递增数列{an}中,a1=2,a2=4,且a2n﹣1 , a2n , a2n+1成等差数列,a2n , a2n+1 , a2n+2成等比数列,n=1,2,3,…. (Ⅰ)(ⅰ)求证:数列 ![]() 为等差数列;
为等差数列;
(ⅱ)求数列{an}的通项公式.
(Ⅱ)设数列 ![]() 的前n项和为Sn , 证明:Sn>
的前n项和为Sn , 证明:Sn> ![]() ,n∈N* .
,n∈N* .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,为迎接校庆,我校准备在直角三角形ABC内的空地上植造一块“绿地△ABD”,规划在△ABD的内接正方形BEFG内种花,其余地方种草,若AB=a,∠DAB=θ,种草的面积为S1 , 种花的面积为S2 , 比值 ![]() 称为“规划和谐度”.
称为“规划和谐度”.
(1)试用a,θ表示S1 , S2;
(2)若a为定值,BC足够长,当θ为何值时,“规划和谐度”有最小值,最小值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,平面A1BC⊥侧面A1B1BA,且AA1=AB=BC=2,则AC与平面A1BC所成角为( ) 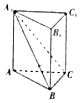
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在等腰直角△ABO中,设 ![]() =
= ![]() ,
, ![]() =
= ![]() ,|
,| ![]() |=|
|=| ![]() |=1,C为AB上靠近A点的三等分点,过C作AB的垂线l,设P为垂线上任一点,
|=1,C为AB上靠近A点的三等分点,过C作AB的垂线l,设P为垂线上任一点, ![]() =
= ![]() ,则
,则 ![]() (
( ![]() ﹣
﹣ ![]() )=( )
)=( ) 
A.![]()
B.﹣ ![]()
C.﹣ ![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C所对的边分别为a、b、c,设向量 ![]() =(a,c),
=(a,c), ![]() =(cosC,cosA).
=(cosC,cosA).
(1)若 ![]() ∥
∥ ![]() ,a=
,a= ![]() c,求角A;
c,求角A;
(2)若 ![]()
![]() =3bsinB,cosA=
=3bsinB,cosA= ![]() ,求cosC的值.
,求cosC的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com