
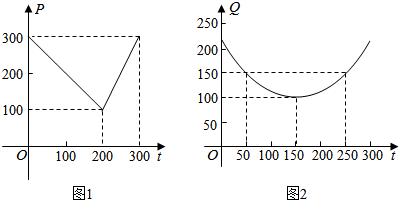
分析 (1)通过图1分别计算0≤t≤200、200<t≤300时可得分段函数,通过图2利用待定系数法计算即得结论;
(2)通过设t时刻的纯收益为h(t),利用h(t)=f(t)-g(t),分0≤t≤200、200<t≤300两种情况配方计算即得结论.
解答 解:(1)由图1可得市场售价与时间的函数关系为f(t)=$\left\{\begin{array}{l}{300-t,}&{0≤t≤200}\\{2t-300,}&{200<t≤300}\end{array}\right.$,
由图2可得种植成本与时间的函数关系式为g(t)=$\frac{1}{200}$(t-150)2+100,0≤t≤300;
(2)设t时刻的纯收益为h(t),则h(t)=f(t)-g(t),
即h(t)=$\left\{\begin{array}{l}{-\frac{1}{200}{t}^{2}+\frac{1}{2}t+\frac{175}{2},}&{0≤t≤200}\\{-\frac{1}{200}{t}^{2}+\frac{7}{2}t-\frac{1025}{2},}&{200<t≤300}\end{array}\right.$,
当0≤t≤200时,配方整理得h(t)=-$\frac{1}{200}$(t-50)2+100,
所以,当t=50时,h(t)取得区间[0,200]上的最大值100;
当200<t≤300时,配方整理得h(t)=-$\frac{1}{200}$(t-350)2+100,
所以,当t=300时,h(t)取得区间(200,300]上的最大值87.5;
综上所述,纯收益最大值为100,此时t=50,即从二月一日开始的第50天时,上市的西红柿收益最大.
点评 本题考查函数模型的选择与应用,考查分析问题、解决问题的能力,注意解题方法的积累,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\frac{{\sqrt{7}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 3 | 4 | 5 | 6 | 7 |
| y | 20 | 30 | 30 | 40 | 60 |
| A. | (5,36) | B. | (5,35) | C. | (5,30) | D. | (4,30) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1:2:3 | B. | 3:2:1 | C. | 1:$\sqrt{3}$:2 | D. | 2:$\sqrt{3}$:1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com