练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．圆x2+y2=1与圆（x-2）2+（y-2）2=5的位置关系为（　　）
    A．内切B．相交C．外切D．相离

    分析 根据两圆的圆心距大于半径之差，而小于半径之和，可得两圆相交．

    解答 解：两圆x2+y2=1与圆（x-2）2+（y-2）2=5的圆心距为2$\sqrt{2}$，
    它大于半径之差$\sqrt{5}$-1，而小于半径之和$\sqrt{5}$+1，
    故两圆相交，
    故选B．

    点评 本题主要考查圆和圆的位置关系的判定，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    14．复数$z=\frac{i}{1-i}$的共轭复数的模为（　　）
    A．$\frac{1}{2}$B．$\frac{{\sqrt{2}}}{2}$C．1D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．设函数f（x）=|x+1|-m|x-2|．
    （Ⅰ）若m=1，求函数f（x）的值域；
    （Ⅱ）若m=-1，求不等式f（x）＞3x的解集．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

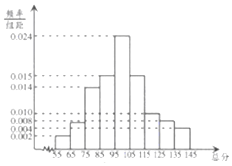    12．从某市统考的学生数学考试卷中随机抽查100份数学试卷作为样本，分别统计出这些试卷总分，由总分得到如下的频率分布直方图．
    （1）求这100份数学试卷的样本平均分$\overline x$和样本方差s2
    （同一组中的数据用该组区间的中点值作代表）
    （2）由直方图可以认为，这批学生的数学总分Z服从正态分布N（μ，σ2），其中μ近似为样本平均数$\overline x$，σ2近似为样本方差s2．
    ①利用该正态分布，求P（81＜z＜119）；
    ②记X表示2400名学生的数学总分位于区间（81，119）的人数，利用①的结果，求EX（用样本的分布区估计总体的分布）．
    附：$\sqrt{366}$≈19，$\sqrt{326}$≈18，若Z=～N（μ，2），则P（μ-σ2），则P（μ-σ＜Z＜μ+σ）=0.6826，P（μ-2σ＜Z＜μ+2σ）=0.9544．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

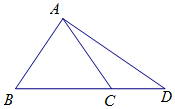    19．已知△ABC是等边三角形，D在BC的延长线上，且CD=2，${S_{△ABD}}=6\sqrt{3}$．
    （Ⅰ）求AB的长；
    （Ⅱ）求sin∠CAD的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知p：-2≤x≤10，q：x2-2x+1-m2≤0（m＞0），若￢p是￢q的必要非充分条件，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．下列命题中不正确的是（　　）
    A．如果平面α⊥平面 γ，平面β⊥平面 γ，α∩β=l，那么l⊥γ
    B．如果平面α⊥平面 β，那么平面α内一定存在直线平行于平面β
    C．如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面β
    D．如果平面α⊥平面 β，过α内任意一点作交线的垂线，那么此垂线必垂直于β

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的短半轴长为1，离心率为$\frac{\sqrt{3}}{2}$
    （1）求椭圆C的方程
    （2）直线l与椭圆C有唯一公共点M，设直线l的斜率为k，M在椭圆C上移动时，作OH⊥l于H（O为坐标原点），当|OH|=$\frac{4}{5}$|OM|时，求k的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．抛物线 M：y2=2px（p＞0）与椭圆 $N：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$有相同的焦点F，抛物线M与 椭圆N交于A，B，若F，A，B共线，则椭圆N的离心率等于$\sqrt{2}$-1．

    查看答案和解析>>

    同步练习册答案