
分析 (1)先求出B,由此利用交集、补集、并集的概念能求出A∩B、(∁RB)∪A.
(2)由C={x|a≤x≤a+1},C⊆B,利用子集的概念能求出实数a的取值范围是[4,7].
解答 解:(1)∵集合A={x|3≤x≤6,B={y|y=2x,2≤x<3}={y|4≤y<8},
∴A∩B={x|4≤x≤6},
∁RB={x|x<4或x>8},(∁RB)∪A=(-∞,6)∪[8,+∞).
(2)∵C={x|a≤x≤a+1},C⊆B,
∴$\left\{\begin{array}{l}{a≥4}\\{a+1≤8}\end{array}\right.$,解得4≤a≤7,
∴实数a的取值范围是[4,7].
点评 本题考查交集、补集、并集、实数的取值范围的求法,是基础题,解题时要注意交集、补集、并集、子集等基本概念的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | .{1,2} | B. | {1} | C. | {-1,1} | D. | .∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
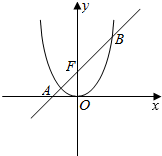 如图,已知抛物线C:x2=2py(0<p<4),其上一点M(4,y0)到其焦点F的距离为5,过焦点F的直线l与抛物线C交于A,B左、右两点.
如图,已知抛物线C:x2=2py(0<p<4),其上一点M(4,y0)到其焦点F的距离为5,过焦点F的直线l与抛物线C交于A,B左、右两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,棱长都相等的平行六面体ABCD-A′B′C′D′中,∠DAB=∠A′AD=∠A′AB=60°,则二面角A′-BD-A的余弦值为( )
如图,棱长都相等的平行六面体ABCD-A′B′C′D′中,∠DAB=∠A′AD=∠A′AB=60°,则二面角A′-BD-A的余弦值为( )| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | -$\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{y}^{2}}{169}$+$\frac{{x}^{2}}{25}$=1(x≠0) | B. | $\frac{{y}^{2}}{169}$+$\frac{{x}^{2}}{144}$=1(x≠0) | ||
| C. | $\frac{{x}^{2}}{169}$+$\frac{{y}^{2}}{25}$=1(y≠0) | D. | $\frac{{y}^{2}}{169}$+$\frac{{x}^{2}}{25}$=1(y≠0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (8,+∞) | B. | (4,+∞) | C. | (-∞,8) | D. | (-∞,4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com