
有一座大桥既是交通拥挤地段,又是事故多发地段,为了保证安全,交通部门规定.大桥上的车距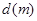 与车速
与车速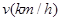 和车长
和车长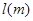 的关系满足:
的关系满足: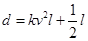 (
( 为正的常数),假定车身长为
为正的常数),假定车身长为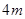 ,当车速为
,当车速为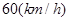 时,车距为2.66个车身长.
时,车距为2.66个车身长.
写出车距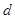 关于车速
关于车速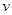 的函数关系式;
的函数关系式;
应规定怎样的车速,才能使大桥上每小时通过的车辆最多?
科目:高中数学 来源: 题型:解答题
已知某公司生产品牌服装的年固定成本是10万元,每生产千件,须另投入2 7万元,设该公司年内共生产该品牌服装x千件并全部销售完,每千件的销售收入为R(x)万元,且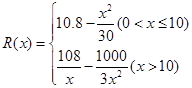
(1)写出年利润W(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获利润最大?(注:年利润=年销售收入 年总成本)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知一家公司生产某种产品的年固定成本为10万元,每生产1千件该产品需另投入2.7万元,设该公司一年内生产该产品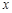 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为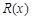 万元,且
万元,且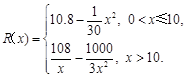
(Ⅰ)写出年利润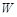 (万元)关于年产量
(万元)关于年产量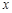 (千件)的函数解析式;
(千件)的函数解析式;
(Ⅱ)年产量为多少千件时,该公司在这一产品的产销过程中所获利润最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com