
已知函数 且
且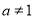 .
.
(1)求函数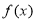 的定义域;
的定义域;
(2)判断 的奇偶性并予以证明.
的奇偶性并予以证明.
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源:2016届河南省郑州市高一上学期期末考试数学试卷(解析版) 题型:选择题
经过点 的直线的斜率等于1,则m的值为( )
的直线的斜率等于1,则m的值为( )
A. 1 B. 4 C. 1或3 D. 1或4
查看答案和解析>>
科目:高中数学 来源:2016届河南周口中英文学校高一下第一次月考数学试卷(解析版) 题型:选择题
某单位有老年人28人,中年人54人,青年人81人.为了调查他们的身体状况,需从他们中抽取一个容量为36的样本,最适合抽取样本的方法是( )
A.简单随机抽样
B.系统抽样
C.分层抽样
D.先从老年人中剔除一人,然后分层抽样
查看答案和解析>>
科目:高中数学 来源:2016届河北省邯郸市高一上学期期末考试数学试卷(解析版) 题型:解答题
已知函数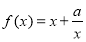 (
(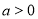 ).
).
(1)证明:当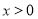 时,
时,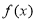 在
在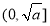 上是减函数,在
上是减函数,在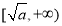 上是增函数,并写出当
上是增函数,并写出当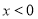 时
时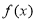 的单调区间;
的单调区间;
(2)已知函数 ,函数
,函数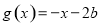 ,若对任意
,若对任意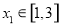 ,总存在
,总存在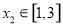 ,使得
,使得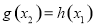 成立,求实数
成立,求实数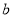 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2016届河北省邯郸市高一上学期期末考试数学试卷(解析版) 题型:选择题
已知函数 ,若关于
,若关于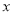 的方程
的方程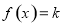 有两个不同的根,则实数
有两个不同的根,则实数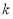 的取值范围是( )
的取值范围是( )
A.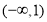 B.
B.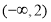 C.
C. D.
D.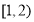
查看答案和解析>>
科目:高中数学 来源:2016届江西鹰潭市高一上学期期末考试理科数学试卷(解析版) 题型:选择题
函数f(x)的定义域为D,满足:①f(x)在D内是单调函数;②存在[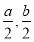 ]
]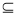 D,使得f(x)在[
D,使得f(x)在[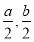 ]上的值域为[a,b],那么就称函数y=f(x)为“优美函数”,若函数f(x)=logc(cx-t)(c>0,c≠1)是“优美函数”,则t的取值范围为( )
]上的值域为[a,b],那么就称函数y=f(x)为“优美函数”,若函数f(x)=logc(cx-t)(c>0,c≠1)是“优美函数”,则t的取值范围为( )
A. (0,1) B. (0,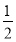 ) C. (-∞,
) C. (-∞,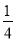 ) D. (0,
) D. (0,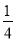 )
)
查看答案和解析>>
科目:高中数学 来源:2016届江西省赣州市六校高一上学期期末联考数学试卷(解析版) 题型:选择题
如右图,点 在半径为
在半径为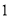 的半圆上运动,
的半圆上运动,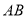 是直径,当
是直径,当 沿半圆弧从
沿半圆弧从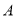 到
到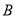 运动时,点
运动时,点 经过的路程
经过的路程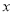 与
与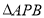 的面积
的面积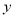 的函数
的函数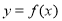 的图像是下图中的( )
的图像是下图中的( )


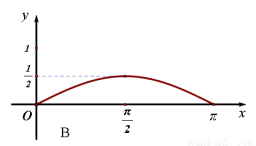


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com