
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() :
: ![]() 的左焦点是
的左焦点是![]() ,离心率为
,离心率为![]() ,且
,且![]() 上任意一点
上任意一点![]() 到
到![]() 的最短距离为
的最短距离为![]() .
.
(1)求![]() 的方程;
的方程;
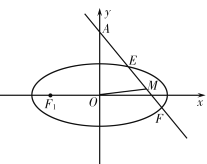
(2)过点![]() 的直线
的直线![]() (不过原点)与
(不过原点)与![]() 交于两点
交于两点![]() 、
、![]() ,
, ![]() 为线段
为线段![]() 的中点.
的中点.
(i)证明:直线![]() 与
与![]() 的斜率乘积为定值;
的斜率乘积为定值;
(ii)求![]() 面积的最大值及此时
面积的最大值及此时![]() 的斜率.
的斜率.
【答案】(1)![]() ;(2)(i)见解析;(ii)
;(2)(i)见解析;(ii)![]() 面积的最大值是
面积的最大值是![]() ,此时
,此时![]() 的斜率为
的斜率为![]() .
.
【解析】试题分析:(1)由题设可以得到关于![]() 的方程组为
的方程组为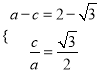 ,从而
,从而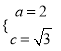 ,故
,故![]() ,所以椭圆
,所以椭圆![]() 的方程为
的方程为![]() .(2)设直线
.(2)设直线![]() 为:
为: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,联立直线的方程和椭圆的方程并消元后可以得到
,联立直线的方程和椭圆的方程并消元后可以得到![]() ,利用韦达定理得到
,利用韦达定理得到![]() ,故
,故![]() ,从而
,从而![]() 为定值.利用弦长公式和点到直线的距离可得
为定值.利用弦长公式和点到直线的距离可得![]() ,令
,令![]() ,从而
,从而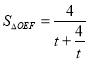 ,最后利用基本不等式可以得到面积的最大值为
,最后利用基本不等式可以得到面积的最大值为![]() 且此时
且此时![]() 也就是
也就是![]() .
.
解析:(1)由题意得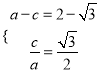 ,解得
,解得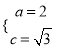 ,∴
,∴![]() ,
, ![]() ,∴椭圆
,∴椭圆![]() 的方程为
的方程为![]() .
.
(2)(i)设直线![]() 为:
为: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,由题意得
,由题意得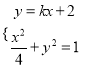 ,
,
∴![]() ,∴
,∴![]() ,即
,即![]() ,由韦达定理得:
,由韦达定理得: ![]() ,
, ![]() ,∴
,∴![]() ,
, ![]() ,∴
,∴![]() ,∴
,∴![]() ,∴直线
,∴直线![]() 与
与![]() 的斜率乘积为定值.
的斜率乘积为定值.
(ii)由(i)可知: ![]()
![]()
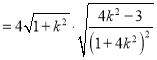
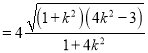 ,又点
,又点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
∴![]() 的面积
的面积![]()
![]()
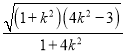
![]() ,令
,令![]() ,则
,则![]() ,∴
,∴![]()
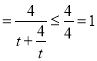 ,当且仅当
,当且仅当![]() 时等号成立,此时
时等号成立,此时![]() ,且满足
,且满足![]() ,∴
,∴![]() 面积的最大值是
面积的最大值是![]() ,此时
,此时![]() 的斜率为
的斜率为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 中,侧面
中,侧面![]() 是边长为2的菱形,且
是边长为2的菱形,且![]() ,
, ![]() ,四棱锥
,四棱锥![]() 的体积为2,点
的体积为2,点![]() 在平面
在平面![]() 内的正投影为
内的正投影为![]() ,且
,且![]() 在
在![]() 上,点
上,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
(Ⅰ)证明:直线![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家举行大型的促销活动,经测算某产品当促销费用为![]() 万元时,销售量
万元时,销售量![]() 万件满足
万件满足![]() (其中
(其中![]() ,
, ![]() 为正常数),现假定生产量与销售量相等,已知生产该产品
为正常数),现假定生产量与销售量相等,已知生产该产品![]() 万件还需投入成本
万件还需投入成本![]() 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为![]() 万元/万件.
万元/万件.
(1)将该产品的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数;
万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,等边三角形![]() 的边长为
的边长为![]() ,且其
,且其
三个顶点均在抛物线![]() 上.
上.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)设动直线![]() 与抛物线
与抛物线![]() 相切于点
相切于点![]() ,与直线
,与直线![]()
相交于点![]() .证明以
.证明以![]() 为直径的圆恒过
为直径的圆恒过![]() 轴上某定点.
轴上某定点.

查看答案和解析>>
科目:高中数学 来源: 题型:
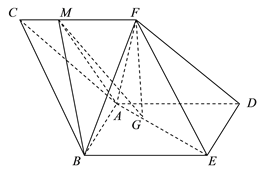
【题目】一装有水的直三棱柱ABC-A1B1C1容器(厚度忽略不计),上下底面均为边长为5的正三角形,侧棱为10,侧面AA1B1B水平放置,如图所示,点D、E、F、G分别在棱CA、CB、C1B1、C1A1上,水面恰好过点D,E,F,C,且CD=2

(1)证明:DE∥AB;
(Ⅱ)若底面ABC水平放置时,求水面的高
查看答案和解析>>
科目:高中数学 来源: 题型:
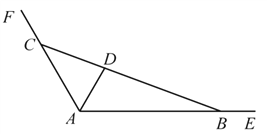
【题目】如图,某大型景区有两条直线型观光路线![]() ,
, ![]() ,
,![]() ,点
,点![]() 位于
位于![]() 的平分线上,且与顶点
的平分线上,且与顶点![]() 相距1公里.现准备过点
相距1公里.现准备过点![]() 安装一直线型隔离网
安装一直线型隔离网![]() (
(![]() 分别在
分别在![]() 和
和![]() 上),围出三角形区域
上),围出三角形区域![]() ,且
,且![]() 和
和![]() 都不超过5公里.设
都不超过5公里.设![]() ,
, ![]() (单位:公里).
(单位:公里).
(Ⅰ)求![]() 的关系式;
的关系式;
(Ⅱ)景区需要对两个三角形区域![]() ,
, ![]() 进行绿化.经测算,
进行绿化.经测算, ![]() 区城每平方公里的绿化费用是
区城每平方公里的绿化费用是![]() 区域的两倍,试确定
区域的两倍,试确定![]() 的值,使得所需的总费用最少.
的值,使得所需的总费用最少.
查看答案和解析>>
科目:高中数学 来源: 题型:
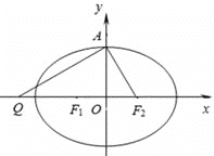
【题目】设椭圆![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,上顶点为A,过点A与
,上顶点为A,过点A与![]() 垂直的直线交
垂直的直线交![]() 轴负半轴于点
轴负半轴于点![]() ,且
,且![]() ,若过
,若过![]() ,
, ![]() ,
, ![]() 三点的圆恰好与直线
三点的圆恰好与直线![]() 相切.过定点
相切.过定点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点(点
两点(点![]() 在点
在点![]() ,
, ![]() 之间).
之间).
(Ⅰ)求椭圆![]() 的方程;(Ⅱ)若实数
的方程;(Ⅱ)若实数![]() 满足
满足![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
在平面直角坐标系xOy 中,曲线C的参数方程为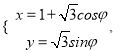 (
(![]() 是参数,0≤
是参数,0≤![]() ≤π),以O 为极点,以x 轴的正半轴为极轴,建立极坐标系.
≤π),以O 为极点,以x 轴的正半轴为极轴,建立极坐标系.
(Ⅰ)求曲线C 的极坐标方程;
(Ⅱ)直线l1,的极坐标方程是2psin(θ+![]() )+
)+![]() =0,直线l2:θ =
=0,直线l2:θ =![]() 与曲线C的交点为P,与直线l1的交点为Q,求线段PQ的长.
与曲线C的交点为P,与直线l1的交点为Q,求线段PQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能生产A类产品5件和B类产品10件,乙种设备每天能生产A类产品6件和B类产品20件。已知设备甲每天的租赁费为200元,设备乙每天的租赁费为300元,现该公司至少要生产A类产品50件,B类产品140件,所需租赁费最少为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com