
【题目】已知复数![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 满足
满足![]() ,
,![]() .
.
(1)若![]() 所对应点
所对应点![]() 在圆
在圆![]() 上,求
上,求![]() 所对应点的轨迹;
所对应点的轨迹;
(2)是否存在这样的直线![]() ,
,![]() 对应点在
对应点在![]() 上,
上,![]() 所对应点也在直线
所对应点也在直线![]() 上?若存在,求出所有这些直线;若不存在,请说明理由.
上?若存在,求出所有这些直线;若不存在,请说明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,大摆锤是一种大型的游乐设备,常见于各大游乐园.游客坐在圆形的座舱中,面向外.通常,大摆锤以压肩作为安全束缚,配以安全带作为二次保险.座舱旋转的同时,悬挂座舱的主轴在电机的驱动下做单摆运动.大摆锤的运行可以使置身其上的游客惊心动魄.今年元旦,小明去某游乐园玩“大摆锤”,他坐在点![]() 处,“大摆锤”启动后,主轴
处,“大摆锤”启动后,主轴![]() 在平面
在平面![]() 内绕点
内绕点![]() 左右摆动,平面
左右摆动,平面![]() 与水平地面垂直,
与水平地面垂直,![]() 摆动的过程中,点
摆动的过程中,点![]() 在平面
在平面![]() 内绕点
内绕点![]() 作圆周运动,并且始终保持
作圆周运动,并且始终保持![]() ,
,![]() ,已知
,已知![]() ,在“大摆锤”启动后,下列
,在“大摆锤”启动后,下列![]() 个结论中正确的是______(请填上所有正确结论的序号).
个结论中正确的是______(请填上所有正确结论的序号).
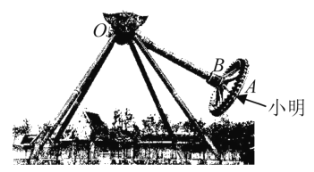
①点![]() 在某个定球面上运动;
在某个定球面上运动;
②线段![]() 在水平地面上的正投影的长度为定值;
在水平地面上的正投影的长度为定值;
③直线![]() 与平面
与平面![]() 所成角的正弦值的最大值为
所成角的正弦值的最大值为![]() ;
;
④直线![]() 与平面
与平面![]() 所成角的正弦值的最大值为
所成角的正弦值的最大值为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位一辆交通车载有8个职工从单位出发送他们下班回家,途中共有甲、乙、丙3个停车点.如果某停车点无人下车,那么该车在这个点就不停车.假设每个职工在每个停车点下车的可能性都是相等的,求下列事件的概率:
(1)该车在某停车点停车;
(2)停车的次数不少于2次;
(3)恰好停车2次.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三台机床各自独立地加工同一种零件,已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率为![]() ,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为
,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为![]() ,甲、丙两台机床加工的零件都是一等品的概率为
,甲、丙两台机床加工的零件都是一等品的概率为![]() .
.
(1)分别求甲、乙、丙三台机床各自加工的零件是一等品的概率;
(2)从甲、乙、丙加工的零件中各取一个检验,求至少有一个一等品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正四棱锥![]() 底面的四个顶点
底面的四个顶点![]() ,
,![]() ,
,![]() ,
,![]() 在球
在球![]() 的同一个大圆上,点
的同一个大圆上,点![]() 在球面上,且已知
在球面上,且已知![]() .
.
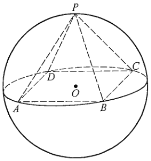
(1)求球![]() 的表面积;
的表面积;
(2)设![]() 为
为![]() 中点,求异面直线
中点,求异面直线![]() 与
与![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在矩形ABCD中,![]() ,
,![]() ,沿矩形对角线BD将
,沿矩形对角线BD将![]() 折起形成四面体ABCD,在这个过程中,现在下面四个结论:①在四面体ABCD中,当
折起形成四面体ABCD,在这个过程中,现在下面四个结论:①在四面体ABCD中,当![]() 时,
时,![]() ;②四面体ABCD的体积的最大值为
;②四面体ABCD的体积的最大值为![]() ;③在四面体ABCD中,BC与平面ABD所成角可能为
;③在四面体ABCD中,BC与平面ABD所成角可能为![]() ;④四面体ABCD的外接球的体积为定值.其中所有正确结论的编号为( )
;④四面体ABCD的外接球的体积为定值.其中所有正确结论的编号为( )
A.①④B.①②C.①②④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】观察不等式:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 由此归纳第
由此归纳第![]() 个不等式为____________;要用数学归纳法证明该不等式,由
个不等式为____________;要用数学归纳法证明该不等式,由![]() 时不等式成立,推证
时不等式成立,推证![]() 时,左边应增加的项数为____________.
时,左边应增加的项数为____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com