
【题目】在直角坐标系xOy中,直线l的参数方程为  (t为参数),再以原点为极点,以x轴正半轴为极轴建立坐标系,并使得它与直角坐标系有相同的长度单位,在该极坐标系中圆C的方程为ρ=4sinθ.
(t为参数),再以原点为极点,以x轴正半轴为极轴建立坐标系,并使得它与直角坐标系有相同的长度单位,在该极坐标系中圆C的方程为ρ=4sinθ.
(1)求圆C的直角坐标方程;
(2)设圆C与直线l交于点A,B,若点M的坐标为(﹣2,1),求|MA|+|MB|的值.
【答案】
(1)解:圆C的方程为ρ=4sinθ,
∴ρ2=4ρsinθ,
∴圆C的直角坐标方程为x2+y2﹣4y=0.
即x2+(y﹣2)2=4
(2)解:|MA|+|MB|的值将直线l的参数方程为 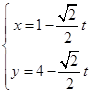 (t为参数)代入圆的方程,得:
(t为参数)代入圆的方程,得:
(1﹣ ![]() t)2+(2﹣
t)2+(2﹣ ![]() )2=4,
)2=4,
整理,得 ![]() ,
,
△=18﹣4=14>0,设t1,t2为方程的两个实根,
则 ![]() ,t1t2=1,∴t1,t2均为正数,
,t1t2=1,∴t1,t2均为正数,
又直线l过M(﹣2,1),
由t的几何意义得:
|MA|+|MB|=|t1|+|t2|= ![]()
【解析】(1)由x=ρcosθ,y=ρsinθ,x2+y2=ρ2,能求出圆C的直角坐标方程.(2)将直线l的参数方程代入圆的直角坐标方程,化简整理,再由韦达定理结合已知条件能求出|MA|+|MD|的值.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=4x焦点为F,点D为其准线与x轴的交点,过点F的直线l与抛物线相交于A,B两点,则△DAB的面积S的取值范围为( )
A.[5,+∞)
B.[2,+∞)
C.[4,+∞)
D.[2,4]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)的图象与g(x)=logax(a>0,且a≠1)的图象关于x轴对称,且g(x)的图象过点(9,2).
(1)求函数f(x)的解析式;
(2)若f(3x1)>f(x+5)成立,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,F1、F2分别是双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的两个焦点,以坐标原点O为圆心,|OF1|为半径的圆与该双曲线左支交于A、B两点,若△F2AB是等边三角形,则双曲线的离心率为( )
=1(a>0,b>0)的两个焦点,以坐标原点O为圆心,|OF1|为半径的圆与该双曲线左支交于A、B两点,若△F2AB是等边三角形,则双曲线的离心率为( ) 
A.![]()
B.2
C.![]() ﹣1
﹣1
D.1+ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂的A、B、C三个不同车间生产同一产品的数量(单位:件)如下表所示.质检人员用分层抽样的方法从这些产品中共抽取6件样品进行检测.
车间 | A | B | C |
数量 | 50 | 150 | 100 |
(1)求这6件样品中来自A、B、C各车间产品的数量;
(2)若在这6件样品中随机抽取2件进行进一步检测,求这2件商品来自相同车间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四名同学根据各自的样本数据研究变量x,y之间的相关关系,并求得回归直线方程,分别得到以下四个结论:
①y与x负相关且 ![]() =2.347x-6.423;②y与x负相关且
=2.347x-6.423;②y与x负相关且 ![]() =-3.476x+5.648;
=-3.476x+5.648;
③y与x正相关且 ![]() =5.437x+8.493;④y与x正相关且
=5.437x+8.493;④y与x正相关且 ![]() =-4.326x-4.578.
=-4.326x-4.578.
其中一定不正确的结论的序号是( )
A.①②
B.②③
C.③④
D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一年级500名学生中,血型为O的有200人,血型为A的有125人,血型为B的有125人,血型为AB型的有50人.为了研究血型与色弱的关系,要从中抽取一个容量为40的样本,应如何抽样?写出血型为AB型的抽样过程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}满足Sn=2n﹣an(n∈N*). (Ⅰ)计算a1 , a2 , a3 , a4 , 并由此猜想通项公式an;
(Ⅱ)用数学归纳法证明(Ⅰ)中的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com