
根据市场调查结果,预测某种家用商品从年初开始的n个月内累积的需求量Sn(万件)近似地满足关系式Sn=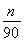 (21n-n2-5)(n=1,2,…,12),按此预测,在本年度内,需求量超过1.5万件的月份是________.
(21n-n2-5)(n=1,2,…,12),按此预测,在本年度内,需求量超过1.5万件的月份是________.
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第3课时练习卷(解析版) 题型:解答题
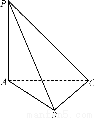
如图,在三棱锥P-ABC中,△PAC,△ABC分别是以A、B为直角顶点的等腰直角三角形,AB=1.现给出三个条件:①PB=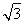 ;②PB⊥BC;③平面PAB⊥平面ABC.试从中任意选取一个作为已知条件,并证明:PA⊥平面ABC;
;②PB⊥BC;③平面PAB⊥平面ABC.试从中任意选取一个作为已知条件,并证明:PA⊥平面ABC;
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第1课时练习卷(解析版) 题型:填空题
如图是正四面体的平面展开图,G,H,M,N分别为DE,BE,EF,EC的中点,在这个正四面体中:
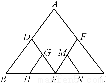
①GH与EF平行;
②BD与MN为异面直线;
③GH与MN成60°角;
④DE与MN垂直.
以上四个命题中,正确命题的是________.(填序号)
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第6课时练习卷(解析版) 题型:填空题
等差数列{an}的前n项和为Sn,已知S10=0,S15=25,则nSn的最小值为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第6课时练习卷(解析版) 题型:解答题
已知数列an=n-16,bn=(-1)n|n-15|,其中n∈N*.
(1)求满足an+1=|bn|的所有正整数n的集合;
(2)若n≠16,求数列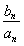 的最大值和最小值;
的最大值和最小值;
(3)记数列{anbn}的前n项和为Sn,求所有满足S2m=S2n(m<n)的有序整数对(m,n).
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第5课时练习卷(解析版) 题型:解答题
已知数列{an}前n项和为Sn,且a2an=S2+Sn对一切正整数都成立.
(1)求a1,a2的值;
(2)设a1>0,数列 前n项和为Tn,当n为何值时,Tn最大?并求出最大值.
前n项和为Tn,当n为何值时,Tn最大?并求出最大值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第5课时练习卷(解析版) 题型:解答题
设C1、C2、…、Cn、…是坐标平面上的一列圆,它们的圆心都在轴的正半轴上,且都与直线y=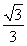 x相切,对每一个正整数n,圆Cn都与圆Cn+1相互外切,以rn表示Cn的半径,已知{rn}为递增数列.
x相切,对每一个正整数n,圆Cn都与圆Cn+1相互外切,以rn表示Cn的半径,已知{rn}为递增数列.
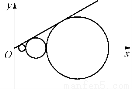
(1)证明:{rn}为等比数列;
(2)设r1=1,求数列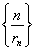 的前n项和.
的前n项和.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第2课时练习卷(解析版) 题型:填空题
已知数列{an}为等差数列,若a1=-3,11a5=5a8,则使前n项和Sn取最小值的n=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com