
���� ��1�����ô��뷨���ɵ�����C1��ֱ�����귽�̣���x=��cos�ȣ�y=��sin�ȣ�x2+y2=��2������ƽ�����ɵõ�����C2��ֱ�����귽�̣�
��2���������C1�IJ�������Ϊ$\left\{\begin{array}{l}{x=\sqrt{3}+\frac{1}{2}m}\\{y=1+\frac{\sqrt{3}}{2}m}\end{array}\right.$��mΪ����������������C2��ֱ�����귽�̣�����Τ�ﶨ�������ɵõ�����ֵ��
��� �⣺��1������C1�IJ�������Ϊ$\left\{\begin{array}{l}{x=\sqrt{3}+t}\\{y=1+\sqrt{3}t}\end{array}\right.$��tΪ��������
��Ϊ$\left\{\begin{array}{l}{t=x-\sqrt{3}}\\{\sqrt{3}t=y-1}\end{array}\right.$����ʽ�������ȥt���ɵã�
����C1��ֱ�����귽��Ϊy-1=$\sqrt{3}$��x-$\sqrt{3}$����
��Ϊy=$\sqrt{3}$x-2��
����C2�ļ����귽��Ϊ��=$\frac{2}{\sqrt{1+3si{n}^{2}��}}$��
����2+3��2sin2��=4��
��x=��cos�ȣ�y=��sin�ȣ�x2+y2=��2��
�ɵ�����C2��ֱ�����귽��Ϊx2+y2+3y2=4��
��Ϊ$\frac{{x}^{2}}{4}$+y2=1��
��2��������C1�IJ�������Ϊ$\left\{\begin{array}{l}{x=\sqrt{3}+\frac{1}{2}m}\\{y=1+\frac{\sqrt{3}}{2}m}\end{array}\right.$��mΪ��������
��������C2��ֱ�����귽��$\frac{{x}^{2}}{4}$+y2=1���ɵã�
��$\sqrt{3}$+$\frac{1}{2}$m��2+4��1+$\frac{\sqrt{3}}{2}$m��2=4��
��Ϊ$\frac{13}{4}$m2+5$\sqrt{3}$m+3=0��
����|MA|•|MB|=|m1|•|m2|=|m1•m2|=$\frac{12}{13}$��
���� ���⿼�鼫���귽�̺�ֱ�����귽�̵Ļ������Լ��������̺�ֱ�����귽�̵Ļ�����ע�����ô��뷨�ͼ������ֱ������Ĺ�ϵ��ͬʱ����ֱ�߲������̵����ã�ע������ļ������壬�����е�����״��⣮


 ������������ϵ�д�
������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
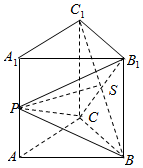 ��ֱ֪������ABC-A1B1C1�ĸ��ⳤ��Ϊa����P�Dz���AA1���е㣬BC1��B1C=S
��ֱ֪������ABC-A1B1C1�ĸ��ⳤ��Ϊa����P�Dz���AA1���е㣬BC1��B1C=S�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
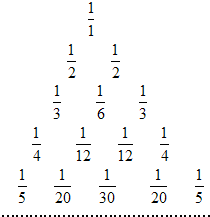 ��ͼ��ʾ������������С�ţ�ٵ��������Ρ����������������ĵ�����ɵģ���n����n���������˵�����Ϊ$\frac{1}{n}$��n��2����ÿ����������һ���������������ĺͣ���$\frac{1}{1}=\frac{1}{2}+\frac{1}{2}$��$\frac{1}{2}=\frac{1}{3}+\frac{1}{6}$��$\frac{1}{3}=\frac{1}{4}+\frac{1}{12}$������
��ͼ��ʾ������������С�ţ�ٵ��������Ρ����������������ĵ�����ɵģ���n����n���������˵�����Ϊ$\frac{1}{n}$��n��2����ÿ����������һ���������������ĺͣ���$\frac{1}{1}=\frac{1}{2}+\frac{1}{2}$��$\frac{1}{2}=\frac{1}{3}+\frac{1}{6}$��$\frac{1}{3}=\frac{1}{4}+\frac{1}{12}$������| A�� | $\frac{1}{2016��2015��2014}$ | B�� | $\frac{1}{2016��2017}$ | C�� | $\frac{1}{2016��2015��1006}$ | D�� | $\frac{1}{2016��2015��1007}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 510 | B�� | 512 | C�� | 1021 | D�� | 1022 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
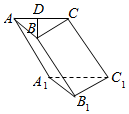 ��ͼ����������ABC-A1B1C1�У���A1B1C1=90�㣬A1B1=B1C1=AA1=2����C�ڵ���A1B1C1�ϵ���ӰA1C1�ߵ��е㣬DΪAC���е㣬��E��CC1�ϣ���$\overrightarrow{{C}_{1}E}$=��$\overrightarrow{{C}_{1}C}$��0���ˣ�1��
��ͼ����������ABC-A1B1C1�У���A1B1C1=90�㣬A1B1=B1C1=AA1=2����C�ڵ���A1B1C1�ϵ���ӰA1C1�ߵ��е㣬DΪAC���е㣬��E��CC1�ϣ���$\overrightarrow{{C}_{1}E}$=��$\overrightarrow{{C}_{1}C}$��0���ˣ�1���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com