
分析 (1)利用4sin2$\frac{A+C}{2}$-cos2B=$\frac{31}{9}$,化简求cosB;
(2)确定cosB=$\frac{1}{3}$,设BC=a,AD=DC=x,则AC=2x,△ABC中,由余弦定理可得4x2=4+a2-$\frac{4}{3}$x①,△ABD和△DBC中,cos∠ADB=-cos∠CDB,可得4x2-2a2=-9②,求出AC,即可求△DBC的面积.
解答 解:(1)∵4sin2$\frac{A+C}{2}$-cos2B=$\frac{31}{9}$,
∴9cos2B-9cosB+2=0,
∴cosB=$\frac{1}{3}$或cosB=$\frac{2}{3}$;
(2)∵角B大于60°,∴cosB=$\frac{1}{3}$
设BC=a,AD=DC=x,则AC=2x,
△ABC中,由余弦定理可得4x2=4+a2-$\frac{4}{3}$a①
△ABD和△DBC中,由余弦定理可得cos∠ADB=$\frac{\frac{17}{4}+{x}^{2}-4}{\sqrt{17}x}$,cos∠CDB=$\frac{\frac{17}{4}+{x}^{2}-{a}^{2}}{\sqrt{17}x}$,
∵∠ADB+∠BDC=180°,
∴cos∠ADB=-cos∠CDB,
∴$\frac{\frac{17}{4}+{x}^{2}-4}{\sqrt{17}x}$=-$\frac{\frac{17}{4}+{x}^{2}-{a}^{2}}{\sqrt{17}x}$,
∴4x2-2a2=-9②,
由①②可得a=3,x=$\frac{3}{2}$,
∴AC=3,
∴S△DBC=$\frac{1}{2}$S△ABC=$\frac{1}{4}×2×3×\frac{2\sqrt{2}}{3}$=$\sqrt{2}$.
点评 本题考查二倍角公式的运用,考查余弦定理,考查三角形面积的计算,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
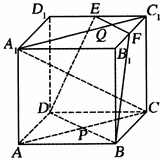 如图:在正方体ABCD-A1B1C1D1中,E,F分别为D1C1,B1C1的中点,AC∩BD=P,A1C1∩EF=Q,直线A1C与平面BDEF的交点为R.
如图:在正方体ABCD-A1B1C1D1中,E,F分别为D1C1,B1C1的中点,AC∩BD=P,A1C1∩EF=Q,直线A1C与平面BDEF的交点为R.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
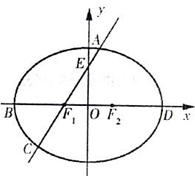 如图,在椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{8}$=1(a>0)中,F1、F2分别为椭圆的左、右焦点,B、D分别为椭圆的左、右顶点,A为椭圆位于第一象限内的部分上的任意一点,直线AF1交椭圆于另一点C,交y轴于点E,且点F1、F2三等分线段BD.
如图,在椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{8}$=1(a>0)中,F1、F2分别为椭圆的左、右焦点,B、D分别为椭圆的左、右顶点,A为椭圆位于第一象限内的部分上的任意一点,直线AF1交椭圆于另一点C,交y轴于点E,且点F1、F2三等分线段BD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com