
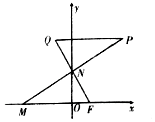
 ��֪��F��1��0��������M��N�ֱ���x�ᣬy�����˶���MN��NF��QΪƽ����һ�㣬$\overrightarrow{NQ}+\overrightarrow{NF}=\overrightarrow 0$������Q��QPƽ����x�ύMN���ӳ����ڵ�P��
��֪��F��1��0��������M��N�ֱ���x�ᣬy�����˶���MN��NF��QΪƽ����һ�㣬$\overrightarrow{NQ}+\overrightarrow{NF}=\overrightarrow 0$������Q��QPƽ����x�ύMN���ӳ����ڵ�P������ �������$\overrightarrow{MN}=��{x��\frac{y}{2}}��$��$\overrightarrow{NF}=��{1��-\frac{y}{2}}��$������$\overrightarrow{MN}•\overrightarrow{NF}=0$���ɵ����P�Ĺ켣����E�ķ��̣�
���������ۣ������Ӧ������������CDF���ABF�����֮�ȣ�
��� �⣺������P��x��y������NΪQ��F���е�ɵ�NΪP��M���е㣬��M��N�ֱ�ΪM��-x��0����$N��{0��\frac{y}{2}}��$$\overrightarrow{MN}=��{x��\frac{y}{2}}��$��$\overrightarrow{NF}=��{1��-\frac{y}{2}}��$��$\overrightarrow{MN}•\overrightarrow{NF}=0$���ɵõ�P�Ĺ켣����Ϊ��y2=4x
��2����ֱ��AB��x��Ľ���G��a��0������$A��{\frac{y_1^2}{4}��{y_1}}��$��$B��{\frac{y_2^2}{4}��{y_2}}��$
��A��B�е�ΪM��x��y����
��AB��x���ֱʱ����kAB=kMG�ɵ�$\frac{4}{{{y_1}+{y_2}}}=\frac{y}{x-a}$
��$\frac{{{y_1}+{y_2}}}{2}=y$����$\frac{4}{2y}=\frac{y}{x-a}$��y2=2��x-a������a=2
��AB��x�ᴹֱʱ��A��B�е�M��G��a��0���غϣ��ʺϷ��̣�
��NΪQ��F���е㣬��֪��Q����x��Ĵ���l��Ϊy2=4x���ߣ�${S_{��CDF}}=\frac{1}{2}|{{y_1}-{y_2}}|•2$��${S_{��ABF}}=\frac{1}{2}|{{y_1}-{y_2}}|•|{a-1}|$=$\frac{1}{2}|{{y_1}-{y_2}}|•1$��
���CDF���ABF�����֮��Ϊ2��
���� ���⿼��켣���̣���������֪ʶ�����ã�����������۵���ѧ˼�룬�����е��⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ֱ������ABC-A1B1C1�У�AB=AC=AA1=4��DΪBB1��һ�㣬EΪAC��һ�㣬��B1D=CE=1��BE=$\sqrt{7}$��
��ͼ����ֱ������ABC-A1B1C1�У�AB=AC=AA1=4��DΪBB1��һ�㣬EΪAC��һ�㣬��B1D=CE=1��BE=$\sqrt{7}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {3} | B�� | {x|$\frac{1}{2}$��x��1} | C�� | {x|x��1} | D�� | {x|0��x��1} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��{-�ޣ�-1}]��[{0��2\sqrt{2}-1}]$ | B�� | $[{-1��2\sqrt{2}-1}]$ | C�� | ��-�ޣ�-1]�ȣ�0��3] | D�� | [-1��3] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2x+y-12=0 | B�� | x+2y-12=0 | C�� | 2x-y-4=0 | D�� | x-2y+4=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com