
【题目】选修4-4:坐标系与参数方程
直角坐标系中曲线![]() 的参数方程
的参数方程![]() (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点, ![]() 轴正半轴为极轴的极坐标系中,
轴正半轴为极轴的极坐标系中, ![]() 点的极坐标
点的极坐标![]() ,在平面直角坐标系中,直线
,在平面直角坐标系中,直线![]() 经过点
经过点![]() ,倾斜角为
,倾斜角为![]()
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的参数方程;
的参数方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】某公司今年一月份推出新产品A,其成本价为492元/件,经试销调查,销售量与销售价的关系如下表:
销售价(x/元件) | 650 | 662 | 720 | 800 |
销售量(y件) | 350 | 333 | 281 | 200 |
由此可知,销售量y(件)与销售价x(元/件)可近似看作一次函数y=kx+b的关系(通常取表中相距较远的两组数据所得一次函数较为精确).
(1)写出以x为自变量的函数y的解析式及定义域;
(2)试问:销售价定为多少时,一月份销售利润最大?并求最大销售利润和此时的销售量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知A为左顶点,F是左焦点,l交OA的延长线于点B,点P,Q在椭圆上,有PD⊥l于点D,QF⊥AO,则椭圆的离心率是① ![]() ; ②
; ② ![]() ; ③
; ③ ![]() ; ④
; ④ ![]() ; ⑤
; ⑤ ![]() 其中正确的是( )
其中正确的是( )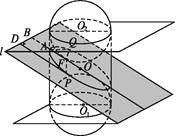
A.①②
B.①③④
C.②③⑤
D.①②③④⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某辆汽车以x km/h的速度在高速公路上匀速行驶(考虑到高速公路行车安全要求60≤x≤120)时,每小时的油耗(所需要的汽油量)为![]() ,其中k为常数,若汽车以120km/h的速度行驶时,每小时的油耗为11.5L.
,其中k为常数,若汽车以120km/h的速度行驶时,每小时的油耗为11.5L.
(1)求k的值;
(2)求该汽车每小时油耗的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,
点, ![]() 为弦
为弦![]() 的中点,直线
的中点,直线![]() 分别与直线
分别与直线![]() 和直线
和直线![]() 交于
交于![]() 两点.
两点.
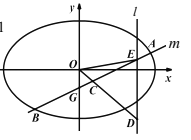
(1)求直线![]() 的斜率和直线
的斜率和直线![]() 的斜率之积;
的斜率之积;
(2)分别记![]() 和
和![]() 的面积为
的面积为![]() ,是否存在正数
,是否存在正数![]() ,使得
,使得![]() 若存在,求出
若存在,求出![]() 的取值;若不存在,说明理由.
的取值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不等式ax2+5x+b>0的解集是{x|2<x<3},则不等式bx2﹣5x+a>0的解集是( )
A.{x|x<﹣3或x>﹣2}
B.{x|x<﹣ ![]() 或x>﹣
或x>﹣ ![]() }
}
C.{x|﹣ ![]() <x<﹣
<x<﹣ ![]() }
}
D.{x|﹣3<x<﹣2}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx﹣x2+1.
(Ⅰ)若曲线y=f(x)在x=1处的切线方程为4x﹣y+b=0,求实数a和b的值;
(Ⅱ)讨论函数f(x)的单调性;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在[﹣1,1]上的奇函数,且对任意a、b∈[﹣1,1],当a+b≠0时,都有 ![]() >0.
>0.
(1)若a>b,比较f(a)与f(b)的大小;
(2)解不等式f(x﹣ ![]() )<f(x﹣
)<f(x﹣ ![]() );
);
(3)记P={x|y=f(x﹣c)},Q={x|y=f(x﹣c2)},且P∩Q=,求c的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com