
【题目】选修4-4:坐标系与参数方程
已知曲线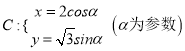 和定点
和定点![]() ,
, ![]() 是此曲线的左、右焦点,以原点
是此曲线的左、右焦点,以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(1)求直线![]() 的极坐标方程;
的极坐标方程;
(2)经过点![]() 且与直线
且与直线![]() 垂直的直线交此圆锥曲线于
垂直的直线交此圆锥曲线于![]() 两点,求
两点,求![]() 的值.
的值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】预计某地区明年从年初开始的前 ![]() 个月内,对某种商品的需求总量
个月内,对某种商品的需求总量 ![]() (万件)近似满足:
(万件)近似满足: ![]() ,且
,且 ![]() )
)
(1)写出明年第 ![]() 个月的需求量
个月的需求量 ![]() (万件)与月份
(万件)与月份 ![]() 的函数关系式,并求出哪个月份的需求量超过
的函数关系式,并求出哪个月份的需求量超过 ![]() 万件;
万件;
(2)如果将该商品每月都投放到该地区 ![]() 万件(不包含积压商品),要保证每月都满足供应,
万件(不包含积压商品),要保证每月都满足供应, ![]() 应至少为多少万件?(积压商品转入下月继续销售)
应至少为多少万件?(积压商品转入下月继续销售)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代的数学名著,书中有如下问题:“今有五人分五钱,令上二人所得与下三人等.问各得几何.”其意思为“已知甲、乙、丙、丁、戊五人分5钱,甲、乙两人所得与丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列.问五人各得多少钱?”(“钱”是古代的一种重量单位).这个问题中,甲所得为( )
A.![]() 钱
钱
B.![]() 钱
钱
C.![]() 钱
钱
D.![]() 钱
钱
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)(其中 ![]() )的图象如图所示,为了得到g(x)=sin2x的图象,则只需将f(x)的图象( )
)的图象如图所示,为了得到g(x)=sin2x的图象,则只需将f(x)的图象( ) 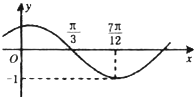
A.向右平移 ![]() 个长度单位
个长度单位
B.向右平移 ![]() 个长度单位
个长度单位
C.向左平移 ![]() 个长度单位
个长度单位
D.向左平移 ![]() 个长度单位
个长度单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=ax2﹣(a+1)x+1
(1)解关于x的不等式f(x)>0;
(2)若对任意的a∈[﹣1,1],不等式f(x)>0恒成立,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若在定义域内存在实数
,若在定义域内存在实数![]() ,满足
,满足![]() ,则称
,则称![]() 为“
为“![]() 类函数”.
类函数”.
(1)已知函数![]() ,试判断
,试判断![]() 是否为“
是否为“![]() 类函数”?并说明理由;
类函数”?并说明理由;
(2)设![]() 是定义在
是定义在![]() 上的“
上的“![]() 类函数”,求是实数
类函数”,求是实数![]() 的最小值;
的最小值;
(3)若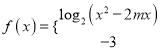
![]() 为其定义域上的“
为其定义域上的“![]() 类函数”,求实数
类函数”,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生对一些对数进行运算,如图表格所示:
x | 0.21 | 0.27 | 1.5 | 2.8 |
lgx | 2a+b+c﹣3(1) | 6a﹣3b﹣2(2) | 3a﹣b+c(3) | 1﹣2a+2b﹣c(4) |
x | 3 | 5 | 6 | 7 |
lgx | 2a﹣b(5) | a+c(6) | 1+a﹣b﹣c(7) | 2(a+c)(8) |
x | 8 | 9 | 14 | |
lgx | 3﹣3a﹣3c(9) | 4a﹣2b(10) | 1﹣a+2b(11) |
现在发觉学生计算中恰好有两次地方出错,那么出错的数据是( )
A.(3),(8)
B.(4),(11)
C.(1),(3)
D.(1),(4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com