
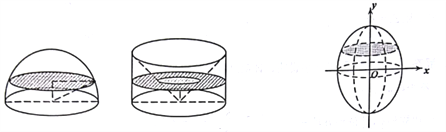
【题目】我国南北朝时间著名数学家祖暅提出了祖暅原理:“幂势既同,则积不容异”.意思是:夹在两平行平面间的两个几何体,被平行于这两个平行平面的任何平面所载,若截得的两个截面面积总相等,则这两个几何体的体积相等.为计算球的体积,构造一个底面半径和高都与球半径相等的圆柱,然后再圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥,运用祖暅原理可证明此几何体与半球体积相等(任何一个平面所载的两个截面面积都相等).将椭圆![]() 绕
绕![]() 轴旋转一周后得一橄榄状的几何体,类比上述方法,运用祖暅原理可求得其体积等于( )
轴旋转一周后得一橄榄状的几何体,类比上述方法,运用祖暅原理可求得其体积等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:高中数学 来源: 题型:
【题目】下列结论中:
①定义在R上的函数f(x)在区间(-∞,0]上是增函数,在区间[0,+∞)上也是增函数,则函数f(x)在R上是增函数;②若f(2)=f(-2),则函数f(x)不是奇函数;③函数y=x-0.5是(0,1)上的减函数;④对应法则和值域相同的函数的定义域也相同;⑤若x0是二次函数y=f(x)的零点,且m<x0<n,那么f(m)f(n)<0一定成立.
写出上述所有正确结论的序号:_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂的固定成本为3万元,该工厂每生产100台某产品的生产成本为1万元,设生产该产品
![]() (百台),其总成本为
(百台),其总成本为![]() 万元(总成本=固定成本+生产成本),并且销售收入
万元(总成本=固定成本+生产成本),并且销售收入![]() 满足
满足![]() ,假设该产品产销平衡,根据上述统计数据规律求:
,假设该产品产销平衡,根据上述统计数据规律求:
(Ⅰ)要使工厂有盈利,产品数量![]() 应控制在什么范围?
应控制在什么范围?
(Ⅱ)工厂生产多少台产品时盈利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学组织了地理知识竞赛,从参加考试的学生中抽出40名学生,将其成绩(均为整数)分成六组![]() ,
,![]() ,…,
,…,![]() ,其部分频率分布直方图如图所示.观察图形,回答下列问题.
,其部分频率分布直方图如图所示.观察图形,回答下列问题.

(1)求成绩在![]() 的频率,并补全这个频率分布直方图:
的频率,并补全这个频率分布直方图:
(2)估计这次考试的及格率(60分及以上为及格)和平均分;(计算时可以用组中值代替各组数据的平均值)
(3)从成绩在![]() 和
和![]() 的学生中选两人,求他们在同一分数段的概率.
的学生中选两人,求他们在同一分数段的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com