
【题目】已知函数![]() ,其中常数
,其中常数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间.
的单调区间.
(2)设定义在![]() 上的函数
上的函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .当
.当![]() 时,若
时,若![]() 在
在![]() 内恒成立,则称
内恒成立,则称![]() 为函数
为函数![]() 的“类对称点”.当
的“类对称点”.当![]() 时,
时,![]() 是否存在“类对称点”?若存在,请求出一个“类对称点”的横坐标;若不存在,请说明理由.
是否存在“类对称点”?若存在,请求出一个“类对称点”的横坐标;若不存在,请说明理由.
【答案】(1)单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() ;(2)存在,横坐标为
;(2)存在,横坐标为![]() .
.
【解析】
(1)由题得![]() 的定义域为
的定义域为![]() ,
,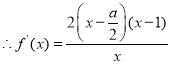 ,由
,由![]() 求得单调增区间,由
求得单调增区间,由![]() 求得单调减区间即可.
求得单调减区间即可.
(2)当![]() 时,
时,![]() ,求得在
,求得在![]() 处的切线方程
处的切线方程![]() ,求得
,求得![]() ,然后根据“类对称点”的定义求“类对称点”的横坐标即可.
,然后根据“类对称点”的定义求“类对称点”的横坐标即可.
解:(1)函数![]() 的定义域为
的定义域为![]() .
.
![]() .
.
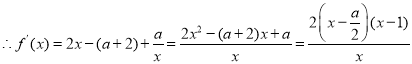
![]() .
.
由![]() ,即
,即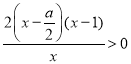 ,得
,得![]() 或
或![]() .
.
由![]() ,得
,得![]() .
.
∴函数![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)存在.
当![]() 时,
时,![]() ,
,
∴在点![]() 处的切线的斜率为
处的切线的斜率为![]() ,
,
∴在点![]() 处的切线方程为
处的切线方程为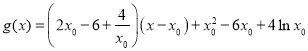 .
.
令![]() ,
,
则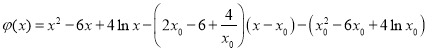 .
.
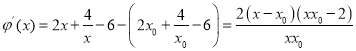 ,
,
令![]() ,得
,得![]() 或
或![]() .
.
①当![]() ,即
,即![]() 时,
时,
令![]() ,则
,则![]() ,
,
∴函数![]() 在区间
在区间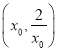 上单调递减,
上单调递减,
又易知![]() ,∴当
,∴当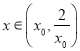 时,
时,![]() ,从而有
,从而有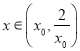 时,
时,![]() .
.
②当![]() ,即
,即![]() 时,
时,
令![]() ,则
,则![]() ,
,
∴函数![]() 在区间
在区间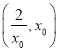 上单调递减,
上单调递减,
∴当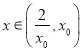 时,
时,![]() ,从而有
,从而有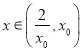 时,
时,![]() .
.
综合①②,当![]() 时,函数
时,函数![]() 不存在“类对称点”.
不存在“类对称点”.
③当![]() 即
即![]() 时,
时,
![]() ,∴函数
,∴函数![]() 在
在![]() 上是增函数.
上是增函数.
若![]() ,则
,则![]() ;
;
若![]() ,则
,则![]() .故
.故![]() 恒成立.
恒成立.
综上,当![]() 时,函数
时,函数![]() 存在“类对称点”,其横坐标为
存在“类对称点”,其横坐标为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】我国新冠肺炎疫情进入常态化,各地有序推进复工复产,下面是某地连续11天复工复产指数折线图,下列说法正确的是( )
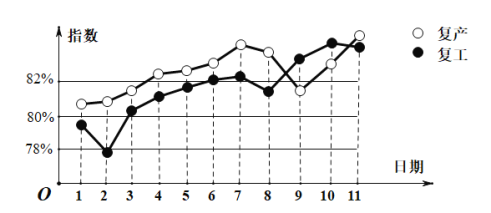
A.这11天复工指数和复产指数均逐日增加;
B.这11天期间,复产指数增量大于复工指数的增量;
C.第3天至第11天复工复产指数均超过80%;
D.第9天至第11天复产指数增量大于复工指数的增量;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构几年前对全国互联网行业进行调查统计,得到整个互联网行业从业人员年龄分布扇形图、90后从事互联网行业岗位分布条形图,则下列结论中不一定正确的是( ).
注:90后指1990-1999年之间出生的人群,80后指1980-1989年之间出生的人群,80前指179年及以前出生的人群.
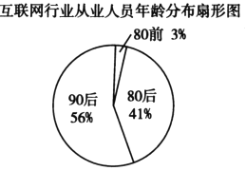

A.互联网行业从业人员中90后占一半以上
B.互联网行业中从事技术岗位的人数超过总人数的20%
C.互联网行业中从事运营岗位的人数90后比80前多
D.互联网行业中从事技术岗位的人数90后比80后多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个特定时段内,以点E为中心的7n mile以内海域被设为警戒水域.点E正北55n mile处有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且与点A相距40![]() n mile的位置B,经过40分钟又测得该船已行驶到点A北偏东
n mile的位置B,经过40分钟又测得该船已行驶到点A北偏东![]() (其中
(其中![]() ,
,![]() )且与点A相距10
)且与点A相距10![]() n mile的位置C.
n mile的位置C.
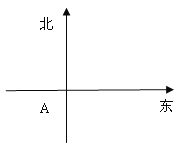
(I)求该船的行驶速度(单位:n mile /h);
(II)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com