
分析 不动点实际上就是方程f(x0)=x0的实数根.二次函数f(x)=x2+ax+4有不动点,是指方程x=x2+ax+4有实根.即方程x=x2+ax+4有两个不同实根,然后根据根列出不等式解答即可.
解答 解:根据题意,f(x)=x2+ax+4在[1,3]恒有两个不同的不动点,得x=x2+ax+4在[1,3]有两个实数根,
即x2+(a-1)x+4=0在[1,3]有两个不同实数根,令g(x)=x2+(a-1)x+4.在[1,3]有两个不同交点,
∴$\left\{\begin{array}{l}g(1)≥0\\ g(3)≥0\\ 1<\frac{1-a}{2}<3\\{(a-1)}^{2}-16>0\end{array}\right.$,即$\left\{\begin{array}{l}a+4≥0\\ 3a+10≥0\\ 1<\frac{1-a}{2}<3\\{(a-1)}^{2}-16>0\end{array}\right.$
解得:a∈$[-\frac{10}{3},-3)$;
故答案为:$[-\frac{10}{3},-3)$.
点评 本题考查了二次函数图象上点的坐标特征、函数与方程的综合运用,解答该题时,借用了一元二次方程的根的判别式与根这一知识点.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
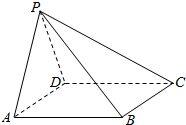 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是菱形,∠BAD=60°,PA=PD=AB=2.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是菱形,∠BAD=60°,PA=PD=AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,将一根长为m的铁丝弯曲围成一个上面是半圆,下方是矩形的形状.
如图,将一根长为m的铁丝弯曲围成一个上面是半圆,下方是矩形的形状.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com