|
|
|
已知f(x)=|x+1|+|x-1|,不等式f(x)<4的解集为M.
(1)求M;
(2)当a,b∈M时,证明:2|a+b|<|4+ab|.
|
|
|
练习册系列答案
相关习题
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
设全集U={x∈Z||x|<3},A={x∈Z|x(x-3)<0},B={-2,-1,2},则A∪(CUB)=
|
| [ ] |
A. |
{1}
|
B. |
{2}
|
C. |
{0,1,2}
|
D. |
{1,2}
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E,F,G分别是PA,PB,BC的中点.
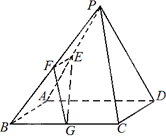
(Ⅰ)求平面EFG与平面ABCD所成锐二面角的大小;
(Ⅱ)若M为线段AB上靠近A的一个动点,问当AM长度等于多少时,直线MF与平面EFG所成角的正弦值等于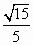 ? ?
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
椭圆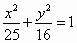 的左右焦点分别为F1,F2,弦AB过F1,若△ABF2的内切圆周长为π,A,B两点的坐标分别为(x1,y1),(x2,y2),则|y1-y2|值为 的左右焦点分别为F1,F2,弦AB过F1,若△ABF2的内切圆周长为π,A,B两点的坐标分别为(x1,y1),(x2,y2),则|y1-y2|值为
|
| [ ] |
A. |
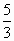
|
B. |
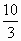
|
C. |
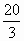
|
D. |
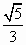
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E,F,G分别是PD,PC,BC的中点.
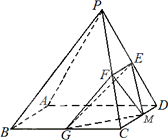
(Ⅰ)求平面EFG⊥平面PAD;
(Ⅱ)若M是线段CD上一点,求三棱锥M-EFG的体积.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
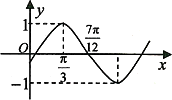
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-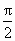 <φ< <φ<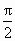 )的部分图象如图所示,则y=f(x)的图象可由函数y=sinx的图象(纵坐标不变)作下述变换得到 )的部分图象如图所示,则y=f(x)的图象可由函数y=sinx的图象(纵坐标不变)作下述变换得到
|
| [ ] |
A. |
先把各点的横坐标缩短到原来的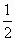 倍,再向右平移 倍,再向右平移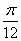 个单位 个单位
|
B. |
先把各点的横坐标伸长到原来的2倍,再向右平移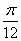 个单位 个单位
|
C. |
先把各点的横坐标缩短到原来的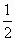 倍,再向右平移 倍,再向右平移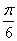 个单位 个单位
|
D. |
先把各点的横坐标伸长到原来的2倍,再向左平移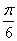 个单位 个单位
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知定义在R上的函数y=f(x)满足f(x+2)=f(x)当-1<x≤1时,f(x)=x3,若函数g(x)=f(x)-loga|x|至少有6个零点,则a的取值范围是
|
| [ ] |
A. |
(1,5)
|
B. |
(0,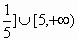
|
C. |
(0,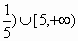
|
D. |
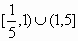
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
设F1,F2是双曲线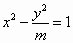 的两个焦点,过点F2作与x轴垂直的直线和双曲线的一个交点为A,满足| 的两个焦点,过点F2作与x轴垂直的直线和双曲线的一个交点为A,满足|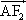 |=| |=|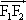 |,则双曲线的离心率为 |,则双曲线的离心率为
|
| [ ] |
A. |
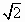
|
B. |
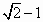
|
C. |
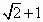
|
D. |
不确定,与m取值有关
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
如图所示的是一个算法的流程图,已知a1=3,输出的结果为7,则a2的值是
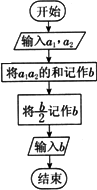
|
| [ ] |
A. |
9
|
B. |
10
|
C. |
11
|
D. |
12
|
|
|
查看答案和解析>>
