
【题目】某市为了宣传环保知识,举办了一次“环保知识知多少”的问卷调查活动(一人答一份).现从回收的年龄在2060岁的问卷中随机抽取了100份, 统计结果如下面的图表所示.
年龄 分组 | 抽取份 数 | 答对全卷的人数 | 答对全卷的人数占本组的概率 |
[20,30) | 40 | 28 | 0.7 |
[30,40) | n | 27 | 0.9 |
[40,50) | 10 | 4 | b |
[50,60] | 20 | a | 0.1 |
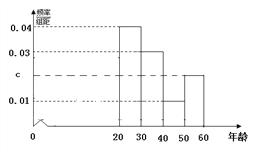
(1)分别求出n, a, b, c的值;
(2)从年龄在[40,60]答对全卷的人中随机抽取2人授予“环保之星”,求年龄在[50,60] 的人中至少有1人被授予“环保之星”的概率.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据频率直方分布图,通过概率的和为1,求求出n,a,b,c的值,
(2)年龄在[40,50)中答对全卷的4人记为A,B,C,D,年龄在[50,60]中答对全卷的2人记为a,b,分别列举出所有的基本事件,根据概率公式计算即可.
试题解析:
(1)因为抽取总问卷为100份,所以n=100-(40+10+20)=30.
年龄在![]() 中,抽取份数为10份,答对全卷人数为4人,所以b=
中,抽取份数为10份,答对全卷人数为4人,所以b=![]() =0.4.
=0.4.
年龄在![]() 中,抽取份数为20份,答对全卷人数占本组的概率为0.1,所以
中,抽取份数为20份,答对全卷人数占本组的概率为0.1,所以![]() =0.1,得
=0.1,得![]() .
.
根据频率直方分布图,得(0.04+0.03+c+0.01)×10=1,解得![]() .
.
(2)因为年龄在![]() 与
与![]() 中答对全卷的人数分别为4人与2人.
中答对全卷的人数分别为4人与2人.
年龄在![]() 中答对全卷的4人记为
中答对全卷的4人记为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,年龄在
,年龄在![]() 中答对全卷的2人记为
中答对全卷的2人记为![]() ,
, ![]() ,则从这6人中随机抽取2人授予“环保之星”奖的所有可能的情况是:
,则从这6人中随机抽取2人授予“环保之星”奖的所有可能的情况是: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,共15种(8分).
,共15种(8分).
其中所抽取年龄在![]() 的人中至少有1人被授予“环保之星”的情况是:
的人中至少有1人被授予“环保之星”的情况是: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 共9种.
共9种.
故所求的概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】对某地区儿童的身高与体重的一组数据,我们用两种模型①![]() ,②
,②![]() 拟合,得到回归方程分别为
拟合,得到回归方程分别为![]() ,
, ![]() ,作残差分析,如表:
,作残差分析,如表:
身高 | 60 | 70 | 80 | 90 | 100 | 110 |
体重 | 6 | 8 | 10 | 14 | 15 | 18 |
| 0.41 | 0.01 | 1.21 | -0.19 | 0.41 | |
| -0.36 | 0.07 | 0.12 | 1.69 | -0.34 | -1.12 |
(Ⅰ)求表中空格内的值;
(Ⅱ)根据残差比较模型①,②的拟合效果,决定选择哪个模型;
(Ⅲ)残差大于![]() 的样本点被认为是异常数据,应剔除,剔除后对(Ⅱ)所选择的模型重新建立回归方程.
的样本点被认为是异常数据,应剔除,剔除后对(Ⅱ)所选择的模型重新建立回归方程.
(结果保留到小数点后两位)
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为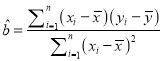 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱柱ABOA′B′O′中,∠AOB=90°,侧棱OO′⊥面OAB,OA=OB=OO′=2.若C为线段O′A的中点,在线段BB′上求一点E,使|EC|最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某颜料公司生产![]() 、
、![]() 两种产品,其中生产每吨
两种产品,其中生产每吨![]() 产品,需要甲染料
产品,需要甲染料![]() 吨,乙染料
吨,乙染料![]() 吨,丙染料
吨,丙染料![]() 吨,生产每吨
吨,生产每吨![]() 产品,需要甲染料
产品,需要甲染料![]() 吨,乙染料
吨,乙染料![]() 吨,丙染料
吨,丙染料![]() 吨,且该公司一天之内甲、乙、丙三种染料的用量分别不超过
吨,且该公司一天之内甲、乙、丙三种染料的用量分别不超过![]() 吨、
吨、![]() 吨、
吨、![]() 吨,如果
吨,如果![]() 产品的利润为
产品的利润为![]() 元/吨,
元/吨, ![]() 产品的利润为
产品的利润为![]() 元/吨,则该颜料公司一天内可获得的最大利润为( )
元/吨,则该颜料公司一天内可获得的最大利润为( )
A. ![]() 元 B.
元 B. ![]() 元 C.
元 C. ![]() 元 D.
元 D. ![]() 元
元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,E、F为棱AD、AB的中点. 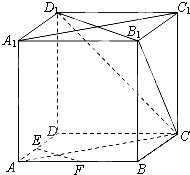
(1)求证:EF∥平面CB1D1;
(2)求证:平面CAA1C1⊥平面CB1D1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱A1B1C1 - ABC中,侧棱AA1丄底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是

A. CC1与B1E是异面直线 B. AC丄平面ABB1A1
C. A1C1∥平面AB1E D. AE与B1C1为异面直线,且AE丄B1C1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=sin(x﹣30°)+cos(x﹣60°),g(x)=2sin2 ![]() .
.
(1)若α为第一象限角且f(α)= ![]() ,求g(α)之值;
,求g(α)之值;
(2)求f(x﹣1080°)≥g(x)在[0,360°]内的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com