
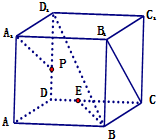
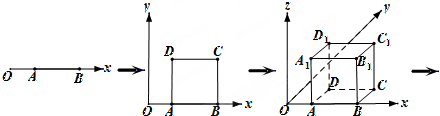
 如图,单位正方体ABCD-A1B1C1D1中,下列说法错误的是
如图,单位正方体ABCD-A1B1C1D1中,下列说法错误的是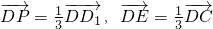 ,则PE∥A1B
,则PE∥A1B
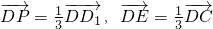 ,则A1P、BE、AD三线共点
,则A1P、BE、AD三线共点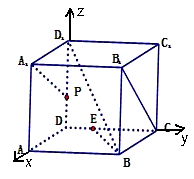
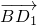 =(-1,-1,1),
=(-1,-1,1), =(-1,0,-1),则
=(-1,0,-1),则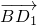 •
• =0∴BD1⊥B1C
=0∴BD1⊥B1C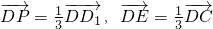 ,则P(0,0,
,则P(0,0, ),E(0,
),E(0, ,0)
,0)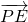 =(0,
=(0, ,-
,- ),
),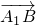 =(0,1,-1)则
=(0,1,-1)则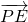 =-
=-
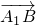 ∴PE∥A1B
∴PE∥A1B ,AC=
,AC= ;
; ,∴点A、C在该球面上的球面距离为
,∴点A、C在该球面上的球面距离为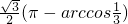 ,则选项C不正确;
,则选项C不正确; A1B,∴A1P、BE共面且相交,假设交点为Q,Q∈A1P,A1P?面A1PD,Q∈BE,BE?面BED
A1B,∴A1P、BE共面且相交,假设交点为Q,Q∈A1P,A1P?面A1PD,Q∈BE,BE?面BED

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
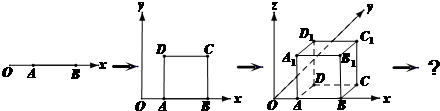
查看答案和解析>>
科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:044
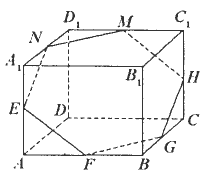
在单位正方体ABCD-A1B1C1D1中E、F、G、H、M、N分别是AA1、AB、BC、C1C、C1D1、D1A1的中点,
(1)证明EFGHMN为平面图形;
(2)求六边形EFGHMN的面积,如图所示.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省三明一中高二(下)第一次月考数学试卷(理科)(解析版) 题型:选择题
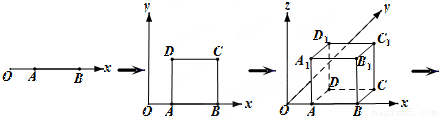
查看答案和解析>>
科目:高中数学 来源:2011年福建省厦门市双十中学高考考前热身数学试卷(理科)(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com