
【题目】2016年9月,第22届鲁台经贸洽谈会在潍坊鲁台会展中心举行,在会展期间某展销商销售一种商品,根据市场调查,每件商品售价x(元)与销量t(万元)之间的函数关系如图所示,又知供货价格与销量呈反比,比例系数为20.(注:每件产品利润=售价﹣供货价格) 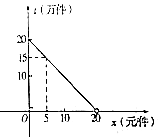
(1)求售价15元时的销量及此时的供货价格;
(2)当销售价格为多少时总利润最大,并求出最大利润.
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
【题目】设l,m是两条不同直线,α是一个平面,则下列四个命题正确的是( )
A.若l⊥m,mα,则l⊥α
B.若l∥α,m∥α,则l∥m
C.若l∥α,mα,则l∥m
D.若l⊥α,l∥m,则m⊥α
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体ABCDEF中,四边形ABCD是正方形,EF∥AB,EF⊥FB,AB=2EF,∠BFC=90°,BF=FC,H为BC的中点.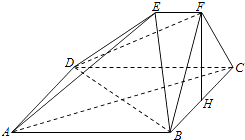
(1)求证:FH∥平面EDB;
(2)求证:AC⊥平面EDB;
(3)解:求二面角B﹣DE﹣C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=﹣ ![]() x3+
x3+ ![]() x2+2ax.
x2+2ax.
(1)若f(x)在( ![]() ,+∞)上是单调减函数,求实数a的取值范围.
,+∞)上是单调减函数,求实数a的取值范围.
(2)当0<a<2时,f(x)在[1,4]上的最小值为﹣ ![]() ,求f(x)在该区间的最大值.
,求f(x)在该区间的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,平面
中,平面![]() 平面
平面![]() ,四边形
,四边形![]() 为菱形,点
为菱形,点![]() 是棱
是棱![]() 上不同于
上不同于![]() ,
, ![]() 的点,平面
的点,平面![]() 与棱
与棱![]() 交于点
交于点![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)求证: ![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求证: ![]() 平面
平面![]() ;
;
(Ⅲ)若二面角![]() 为
为![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)═log2( ![]() +a).
+a).
(1)若f(1)<2,求实数a的取值范围;
(2)设函数g(x)=f(x)﹣log2[(a﹣4)x+2a﹣5],讨论函数g(x)的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知偶函数f(x)的定义域为R,且在(﹣∞,0)上是增函数,则f(﹣ ![]() )与f(a2﹣a+1)的大小关系为( )
)与f(a2﹣a+1)的大小关系为( )
A.f(﹣ ![]() )<f(a2﹣a+1)
)<f(a2﹣a+1)
B.f(﹣ ![]() )>f(a2﹣a+1)??
)>f(a2﹣a+1)??
C.f(﹣ ![]() )≤f(a2﹣a+1)
)≤f(a2﹣a+1)
D.f(﹣ ![]() )≥f(a2﹣a+1)
)≥f(a2﹣a+1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在直角梯形ABCD中,AB∥CD,∠BCD=90°,BC=CD=2,AF=BF,EC∥FD,FD⊥底面ABCD,M是AB的中点. 
(1)求证:平面CFM⊥平面BDF;
(2)点N在CE上,EC=2,FD=3,当CN为何值时,MN∥平面BEF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com