
分析 (1)当a=2时,求出g(x)=0的解,即可解关于x的方程g(ex)=0(其中e为自然对数的底数);
(2)φ(x)=f(x)+g(x)=lnx+ax+$\frac{a-1}{x}$-3,φ′(x)=$\frac{[ax-(a-1)](x+1)}{{x}^{2}}$,分类讨论,利用导数的正负,求函数φ(x)=f(x)+g(x)的单调增区间;
(3)判断h(x)不存在最小值,即可得出结论.
解答 解:(1)当a=2时,g(x)=0,可得x=$\frac{1}{2}或$1,
g(ex)=0,可得ex=$\frac{1}{2}$或ex=1,
∴x=-ln2或0;
(2)φ(x)=f(x)+g(x)=lnx+ax+$\frac{a-1}{x}$-3,φ′(x)=$\frac{[ax-(a-1)](x+1)}{{x}^{2}}$
①a=0,φ′(x)=$\frac{x+1}{{x}^{2}}$>0,函数的单调递增区间是(0,+∞);
②a=1,φ′(x)=$\frac{x+1}{{x}^{2}}$•x>0,函数的单调递增区间是(0,+∞);
③0<a<1,x=$\frac{a-1}{a}$<0,函数的单调递增区间是(0,+∞);
④a>1,x=$\frac{a-1}{a}$>0,函数的单调递增区间是($\frac{a-1}{a}$,+∞);
⑤a<0,x=$\frac{a-1}{a}$>0,函数的单调递增区间是(0,$\frac{a-1}{a}$);
(3)a=1,h(x)=(x-3)lnx,h′(x)=lnx-$\frac{3}{x}$+1,
h″(x)=$\frac{1}{x}$+$\frac{3}{{x}^{2}}$>0恒成立,∴h′(x)在(0,+∞)上单调递增,
∴存在x0,h′(x0)=0,即lnx0=-1+$\frac{3}{{x}_{0}}$,
h(x)在(0,x0)上单调递减,(x0,+∞)上单调递增,
∴h(x)min=h(x0)=-(x0+$\frac{9}{{x}_{0}}$)+6,
∵h′($\frac{3}{2}$)<0,h′(2)>0,∴x0∈($\frac{3}{2}$,2),
∴h(x0)∈(-$\frac{3}{2}$,-$\frac{1}{2}$),
∴存在λ的最小值0,使得关于x的不等式2λ≥h(x)有解.
点评 本题考查导数知识的综合运用,考查函数的单调性与最值,考查分类讨论的数学思想,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
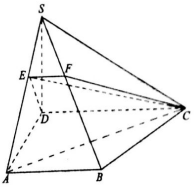 如图,在直角梯形ABCD中,∠ADC=∠BAD=90°,AB=AD=1,CD=2,平面SAD⊥平面ABCD,平面SDC⊥平面ABCD,SD=$\sqrt{3}$,在线段SA上取一点E(不含端点)使EC=AC,截面CDE交SB于点F.
如图,在直角梯形ABCD中,∠ADC=∠BAD=90°,AB=AD=1,CD=2,平面SAD⊥平面ABCD,平面SDC⊥平面ABCD,SD=$\sqrt{3}$,在线段SA上取一点E(不含端点)使EC=AC,截面CDE交SB于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com