
【题目】在△ABC中,分别根据下列条件解三角形,其中有两个解的是( )
A.a=7,b=14,A=30°
B.a=20,b=26,A=150°
C.a=30,b=40,A=30°
D.a=72,b=60,A=135°
【答案】C
【解析】解:对于A:∵a=7,b=14,A=30°,
∴由正弦定理得:sinB= ![]() =
= ![]() =1,
=1,
又B为三角形的内角,
∴B=90°,
故只有一解,本选项不合题意;
对于B:∵a=20,b=26,A=150°,
∴由正弦定理得:sinB= ![]() =
= ![]() =
= ![]() ,
,
又b>a,故 B>A,A为钝角,故△ABC不存在;
对于C:∵a=30,b=40,A=30°,有 ![]() =
= ![]() ,
,
∴sinB= ![]() ,又b>a,故B>A,故B可以是锐角,也可以是钝角,故△ABC有两个解.
,又b>a,故B>A,故B可以是锐角,也可以是钝角,故△ABC有两个解.
对于D:∵a=72,b=60,A=135°,
由正弦定理得:sinB= ![]() =
= ![]() =
= ![]() ,
,
又b<a,故B<A,故B为锐角,故△ABC有唯一解.
故选:C.
由正弦定理可得sinB= ![]() ,根据条件求得sinB的值,根据b与a的大小判断角B的大小,从而判断△ABC的解的个数.
,根据条件求得sinB的值,根据b与a的大小判断角B的大小,从而判断△ABC的解的个数.


科目:高中数学 来源: 题型:
【题目】设正项数列{an}的前n项和为Sn , 且满足4Sn=an2+2an﹣3(n∈N*),则a2016=( )
A.4029
B.4031
C.4033
D.4035
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为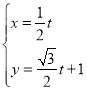 (
(![]() 为参数),曲线
为参数),曲线![]() 的普通方程为
的普通方程为![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(I)求直线![]() 的极坐标方程与曲线
的极坐标方程与曲线![]() 的参数方程;
的参数方程;
(II)设点D在曲线![]() 上,且曲线
上,且曲线![]() 在点D处的切线与直线
在点D处的切线与直线![]() 垂直,试确定点D的坐标.
垂直,试确定点D的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】拖延症总是表现在各种小事上,但日积月累,特别影响个人发展.某校的一个社会实践调查小组,在对该校学生进行“是否有明显拖延症”的调查中,随机发放了110份问卷.对收回的100份有效问卷进行统计,得到如下![]() 列联表:
列联表:

(1)按女生是否有明显拖延症进行分层,已经从40份女生问卷中抽取了8份问卷,现从这8份问卷中再随机抽取3份,并记其中无明显拖延症的问卷的份数为![]() ,试求随机变量
,试求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(2)若在犯错误的概率不超过![]() 的前提下认为无明显拖延症与性别有关,那么根据临界值表,最精确的
的前提下认为无明显拖延症与性别有关,那么根据临界值表,最精确的![]() 的值应为多少?请说明理由.附:独立性检验统计量
的值应为多少?请说明理由.附:独立性检验统计量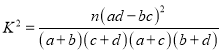 ,其中
,其中![]() .
.
独立性检验临界值表:
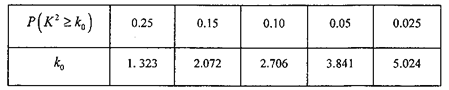
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com