
【题目】设Sn为数列{cn}的前n项和,an=2n , bn=50﹣3n,cn= ![]() .
.
(1)求c4与c8的等差中项;
(2)当n>5时,设数列{Sn}的前n项和为Tn .
(ⅰ)求Tn;
(ⅱ)当n>5时,判断数列{Tn﹣34ln}的单调性.
【答案】
(1)解:∵a4<b4=38,∴c4=38,
∵b8<a8=256,∴c8=256,
∴c4与c8的等差中项为 ![]() =
= ![]() .
.
(2)解:(ⅰ)当n≤5时,an<bn,
则S1=47,S2=91,S3=132,S4=170,S5=205,
当n=5时,an=bn,
则Sn=b1+b2+b3+b4+b5+a6+a7+…+an
=205+ ![]() =2n+1+141.
=2n+1+141.
∴当n>5时,Tn=47+91+132+170+205+(27+141)+(28+141)+…+(2n+1+141)
=645+ ![]() +141(n﹣5)=2n+2+141n﹣188.
+141(n﹣5)=2n+2+141n﹣188.
(ⅱ)设dn=Tn﹣341n=2n+2﹣200n﹣188,
dn+1﹣dn=2n+2﹣200,
当n>5时,2n+2﹣200>0,
∴dn+1>dn,
∴当n>5时,数列{Tn﹣34ln}的单调递增
【解析】1、根据等差中项的定义求得。
2、由题意分情况可得(ⅰ)当n≤5时,可证明当n=5时,an=bn,则Sn=b1+b2+b3+b4+b5+a6+a7+…+an=2n+1+141.当n>5时,Tn==2n+2+141n﹣188。(ⅱ)设dn=Tn﹣341n=2n+2﹣200n﹣188,当n>5时,2n+2﹣200>0,∴dn+1>dn,即可得证当n>5时,数列{Tn﹣34ln}的单调递增。
【考点精析】关于本题考查的数列的前n项和和数列的通项公式,需要了解数列{an}的前n项和sn与通项an的关系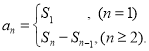 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能得出正确答案.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能得出正确答案.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:
【题目】如图为某校语言类专业N名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的学员数为21人. (Ⅰ)求该专业毕业总人数N和90~95分数段内的人数n;
(Ⅱ)现欲将90~95分数段内的n名人分配到几所学校,从中安排2人到甲学校去,若n人中仅有两名男生,求安排结果至少有一名男生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=lnx+ ![]() x2 .
x2 .
(1)求曲线f(x)在x=1处的切线方程;
(2)设P为曲线f(x)上的点,求曲线C在点P处切线的斜率的最小值及倾斜角α的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设向量 ![]() ,
, ![]() ,
, ![]() 满足|
满足| ![]() |=2,|
|=2,| ![]() +
+ ![]() |=6,|
|=6,| ![]() |=|
|=| ![]() |,且
|,且 ![]() ⊥
⊥ ![]() ,则|
,则| ![]() ﹣
﹣ ![]() |的取值范围为( )
|的取值范围为( )
A.[4,8]
B.[4 ![]() ,8
,8 ![]() ]
]
C.(4,8)
D.(4 ![]() ,8
,8 ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,已知2sinA﹣cosB=2sinBcosC,且角B为钝角.
(1)求角C的大小;
(2)若a=2,b2+c2﹣a2= ![]() bc,求△ABC的面积.
bc,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定圆M: ![]() =16,动圆N过点F
=16,动圆N过点F ![]() 且与圆M相切,记圆心N的轨迹为E.
且与圆M相切,记圆心N的轨迹为E.
(I)求轨迹E的方程;
(Ⅱ)设点A,B,C在E上运动,A与B关于原点对称,且|AC|=|CB|,当△ABC的面积最小时,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】二次函数f(x),又 ![]() 的图象与x轴有且仅有一个公共点,且f′(x)=1﹣2x.
的图象与x轴有且仅有一个公共点,且f′(x)=1﹣2x.
(1)求f(x)的表达式.
(2)若直线y=kx把y=f(x)的图象与x轴所围成的图形的面积二等分,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com