
【题目】在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F. 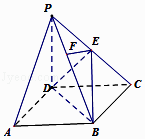
(1)求证PA∥平面EDB;
(2)求二面角C﹣PB﹣D的大小.
【答案】
(1)证明:连结AC,BD,交于点O,连结OE,
∵底面ABCD是正方形,∴O是AC的中点,
∵点E是PC的中点,∴OE∥PA,
∵OE平面EBD,PA平面EBD,
∴PA∥平面EDB
(2)解:以D为原点,DA,DC,DP为x,y,z轴,建立空间直角坐标系,
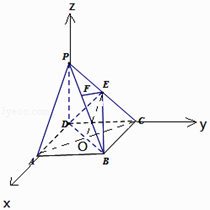
设PD=DC=1,则D(0,0,0),P(0,0,1),
B(1,1,0),C(0,1,0),
![]() =(0,0,1),
=(0,0,1), ![]() =(1,1,0),
=(1,1,0), ![]() =(0,1,﹣1),
=(0,1,﹣1),
![]() =(1,1,﹣1),
=(1,1,﹣1),
设平面PBC的法向量 ![]() =(x,y,z),平面PBD的法向量
=(x,y,z),平面PBD的法向量 ![]() =(a,b,c),
=(a,b,c),
则  ,取y=1,得
,取y=1,得 ![]() =(0,1,1),
=(0,1,1),
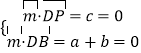 ,取a=1,得
,取a=1,得 ![]() =(1,﹣1,0),
=(1,﹣1,0),
设二面角C﹣PB﹣D的大小为θ,
则cosθ= ![]() =
= ![]() =
= ![]() ,
,
∴θ=60°,
∴二面角C﹣PB﹣D的大小为60°.
【解析】(1)连结AC,BD,交于点O,连结OE,则OE∥PA,由此能证明PA∥平面EDB.(2)以D为原点,DA,DC,DP为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角C﹣PB﹣D的大小.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)=ln(1﹣ ![]() )+1,则f(﹣7)+f(﹣5 )+f(﹣3)+f(﹣1)+f(3 )+f( 5)+f(7 )+f( 9)=( )
)+1,则f(﹣7)+f(﹣5 )+f(﹣3)+f(﹣1)+f(3 )+f( 5)+f(7 )+f( 9)=( )
A.0
B.4
C.8
D.16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=2sin(180°﹣x)+cos(﹣x)﹣sin(450°﹣x)+cos(90°+x).
(1)若f(α)= ![]() α∈(0°,180°),求tanα;
α∈(0°,180°),求tanα;
(2)若f(α)=2sinα﹣cosα+ ![]() ,求sinαcosα的值.
,求sinαcosα的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设 ![]() 、
、 ![]() 为平面向量,若存在不全为零的实数λ,μ使得λ
为平面向量,若存在不全为零的实数λ,μ使得λ ![]() +μ
+μ ![]() =0,则称
=0,则称 ![]() 、
、 ![]() 线性相关,下面的命题中,
线性相关,下面的命题中, ![]() 、
、 ![]() 、
、 ![]() 均为已知平面M上的向量. ①若
均为已知平面M上的向量. ①若 ![]() =2
=2 ![]() ,则
,则 ![]() 、
、 ![]() 线性相关;
线性相关;
②若 ![]() 、
、 ![]() 为非零向量,且
为非零向量,且 ![]() ⊥
⊥ ![]() ,则
,则 ![]() 、
、 ![]() 线性相关;
线性相关;
③若 ![]() 、
、 ![]() 线性相关,
线性相关, ![]() 、
、 ![]() 线性相关,则
线性相关,则 ![]() 、
、 ![]() 线性相关;
线性相关;
④向量 ![]() 、
、 ![]() 线性相关的充要条件是
线性相关的充要条件是 ![]() 、
、 ![]() 共线.
共线.
上述命题中正确的是(写出所有正确命题的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,若A,B,C成等差数列,2a,2b,2c成等比数列,则sinAcosBsinC=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,AF=AB=BC=FE= ![]() AD.
AD. 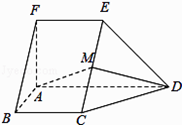
(1)求异面直线BF与DE所成的角的大小;
(2)证明平面AMD⊥平面CDE;
(3)求锐二面角A﹣CD﹣E的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com