
(本题满分14分)给定椭圆 >
> >0
>0 ,称圆心在原点
,称圆心在原点 ,半径为
,半径为 的圆是椭圆
的圆是椭圆 的“伴随圆”.若椭圆
的“伴随圆”.若椭圆 的一个焦点为
的一个焦点为 ,其短轴上的一个端点到
,其短轴上的一个端点到 的距离为
的距离为 .
.
(1)求椭圆 的方程及其“伴随圆”方程;
的方程及其“伴随圆”方程;
(2)若倾斜角为 的直线
的直线 与椭圆C只有一个公共点,且与椭圆
与椭圆C只有一个公共点,且与椭圆 的伴随圆相交于M、N两
的伴随圆相交于M、N两
点,求弦MN的长;
(3)点 是椭圆
是椭圆 的伴随圆上的一个动点,过点
的伴随圆上的一个动点,过点 作直线
作直线 ,使得
,使得 与椭圆
与椭圆 都只有一个公共点,求证:
都只有一个公共点,求证: ⊥
⊥ .
.
解:(1)因为 ,所以
,所以 ,所以椭圆的方程为
,所以椭圆的方程为 ,
,
伴随圆的方程为 . ……………………………… 4分
. ……………………………… 4分
(2)设直线 的方程
的方程 ,由
,由 得
得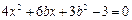
由 得
得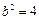 ,圆心到直线
,圆心到直线 的距离为
的距离为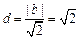
所以 。 ……………………………… 8分
。 ……………………………… 8分
(3)①当 中有一条无斜率时,不妨设
中有一条无斜率时,不妨设 无斜率,
无斜率,
因为 与椭圆只有一个公共点,则其方程为
与椭圆只有一个公共点,则其方程为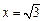 或
或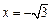 ,
,
当 方程为
方程为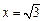 时,此时
时,此时 与伴随圆交于点
与伴随圆交于点
此时经过点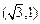 (或
(或 且与椭圆只有一个公共点的另一条直线是
且与椭圆只有一个公共点的另一条直线是 (或
(或 ,即
,即 为
为 (或
(或 ,显然直线
,显然直线 垂直;
垂直;
同理可证 方程为
方程为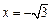 时,直线
时,直线 垂直. ……………………………… 10分
垂直. ……………………………… 10分
②当 都有斜率时,设点
都有斜率时,设点 其中
其中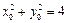 ,
,
设经过点 与椭圆只有一个公共点的直线为
与椭圆只有一个公共点的直线为 ,
,
由 ,消去
,消去 得到
得到 ,
,
即 ,
,  ,
,
经过化简得到: ,
,
因为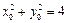 ,所以有
,所以有 ,
,
设 的斜率分别为
的斜率分别为 ,因为
,因为 与椭圆都只有一个公共点,
与椭圆都只有一个公共点,
所以 是关于
是关于 的方程:
的方程: 的两个实数根,
的两个实数根,
因而 ,即
,即 ⊥
⊥ . ……………………………… 14分
. ……………………………… 14分
解析


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
 (本题满分14分)
(本题满分14分)
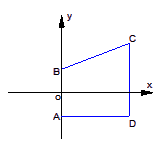
在梯形ABCD中,AB⊥AD,AB∥CD,A、B是两个定点,其坐
标分别为(0,-1)、(0,1),C、D是两个动点,且满足|CD|=|BC|.
(1)求动点C的轨迹E的方程;
(2)试探究在轨迹E上是否存在一点P?使得P到直线y=x-2的
距离最短;
(3)设轨迹E与直线![]() 所围成的图形的
所围成的图形的
面积为S,试求S的最大值。
其它解法请参照给分。
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分14分)本公司计划2008年在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元,甲、乙电视台的广告收费标准分别为![]() 元/分钟和200元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司事来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
元/分钟和200元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司事来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东高一第二次月考数学试卷(解析版) 题型:解答题
(本题满分14分)已知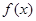 为定义在
为定义在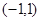 上的奇函数,当
上的奇函数,当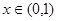 时,
时,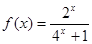 ;
;
(1)求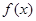 在
在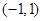 上的解析式;
上的解析式;
(2)试判断函数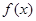 在区间
在区间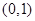 上的单调性,并给出证明.
上的单调性,并给出证明.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市十三校高三上学期第一次联考试题文科数学 题型:解答题
(本题满分14分,第1小题满分7分,第2小题满分7分)
为了研究某种癌细胞的繁殖规律和一种新型抗癌药物的作用,将癌细胞注入一只小白鼠体内进行实验,经检测,癌细胞的繁殖规律与天数的关系如下表.已知这种癌细胞在小白鼠体内的个数超过 时小白鼠将会死亡,注射这种抗癌药物可杀死其体内癌细胞的
时小白鼠将会死亡,注射这种抗癌药物可杀死其体内癌细胞的 .
.
|
天数 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
… |
|
癌细胞个数 |
1 |
2 |
4 |
8 |
16 |
32 |
64 |
… |
(1)要使小白鼠在实验中不死亡,第一次最迟应在第几天注射该种药物?(精确到1天)
(2)若在第10天,第20天,第30天,……给小白鼠注射这种药物,问第38天小白鼠是否仍然存活?请说明理由.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年上海市普通高等学校高三春季招生数学卷 题型:解答题
(本题满分14分)已知抛物线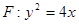
(1)△ABC的三个顶点在抛物线F上,记△ABC的三边AB、BC、CA所在的直线的斜率分别为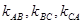 ,若A的坐标在原点,求
,若A的坐标在原点,求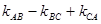 的值;
的值;
(2)请你给出一个以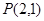 为顶点、其余各顶点均为抛物线F上的动点的多边形,写出各多边形各边所在的直线斜率之间的关系式,并说明理由
为顶点、其余各顶点均为抛物线F上的动点的多边形,写出各多边形各边所在的直线斜率之间的关系式,并说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com