
ЁОЬтФПЁПЙВЯэЕЅГЕШызЁШЊжнвЛжмФъвдРДЃЌвђЦфЁАТЬЩЋГіааЃЌЕЭЬМЛЗБЃЁБЕФРэФюЖјБИЪмШЫУЧЕФЯВАЎЃЌжЕДЫжмФъжЎМЪЃЌФГЛњЙЙЮЊСЫСЫНтЙВЯэЕЅГЕЪЙгУепЕФФъСфЖЮЃЌЪЙгУЦЕТЪЁЂТњвтЖШЕШШ§ИіЗНУцЕФаХЯЂЃЌдкШЋЪаЗЖЮЇФкЗЂЗХ![]() ЗнЕїВщЮЪОэЃЌЛиЪеЕНгааЇЮЪОэ
ЗнЕїВщЮЪОэЃЌЛиЪеЕНгааЇЮЪОэ![]() ЗнЃЌЯжДгжаЫцЛњГщШЁ
ЗнЃЌЯжДгжаЫцЛњГщШЁ![]() ЗнЃЌЗжБ№ЖдЪЙгУепЕФФъСфЖЮЁЂ
ЗнЃЌЗжБ№ЖдЪЙгУепЕФФъСфЖЮЁЂ![]() ~
~![]() ЫъЪЙгУепЕФЪЙгУЦЕТЪЁЂ
ЫъЪЙгУепЕФЪЙгУЦЕТЪЁЂ![]() ~
~![]() ЫъЪЙгУепЕФТњвтЖШНјааЛузмЃЌЕУЕНШчЯТШ§ИіБэИёЃК
ЫъЪЙгУепЕФТњвтЖШНјааЛузмЃЌЕУЕНШчЯТШ§ИіБэИёЃК
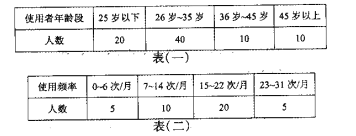
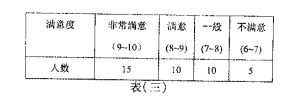
ЃЈЂёЃЉвРОнЩЯЪіБэИёЭъГЩЯТСаШ§ИіЭГМЦЭМаЮЃК
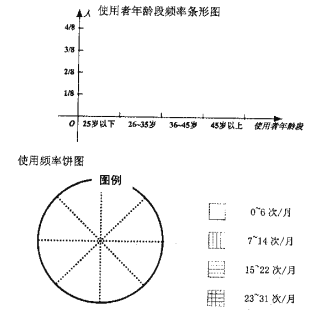
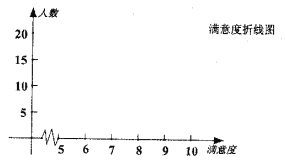
ЃЈЂђЃЉФГГЧЧјЯжгаГЃзЁШЫПк![]() ЭђЃЌЧыгУбљБОЙРМЦзмЬхЕФЫМЯыЃЌЪдЙРМЦФъСфдк
ЭђЃЌЧыгУбљБОЙРМЦзмЬхЕФЫМЯыЃЌЪдЙРМЦФъСфдк![]() Ыъ~
Ыъ~![]() ЫъжЎМфЃЌУПдТЪЙгУЙВЯэЕЅГЕдк
ЫъжЎМфЃЌУПдТЪЙгУЙВЯэЕЅГЕдк![]() ~
~![]() ДЮЕФШЫЪ§.
ДЮЕФШЫЪ§.
ЁОД№АИЁПЃЈЂёЃЉМћНтЮіЃЈЂђЃЉФъСфдк![]() Ыъ
Ыъ![]() ЫъжЎМфЃЌУПдТЪЙгУЙВЯэЕЅГЕдк
ЫъжЎМфЃЌУПдТЪЙгУЙВЯэЕЅГЕдк![]() ДЮжЎМфЕФШЫЪ§дМЮЊ
ДЮжЎМфЕФШЫЪ§дМЮЊ![]() ЭђШЫ
ЭђШЫ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнЪ§ОнМАИїБэИёЖдгІЙиЯЕЬюБэЛђЛЭМЃЈ2ЃЉЯШИљОнФъСфдк![]() Ыъ~
Ыъ~![]() ЫъжЎМфЕФга
ЫъжЎМфЕФга![]() ШЫЃЌеМзмГщШЁШЫЪ§дквЛАыЃЌЕУФГГЧЧј
ШЫЃЌеМзмГщШЁШЫЪ§дквЛАыЃЌЕУФГГЧЧј![]() ЭђШЫПкжаФъСфдк
ЭђШЫПкжаФъСфдк![]() Ыъ~
Ыъ~![]() ЫъжЎМфЕФдМга
ЫъжЎМфЕФдМга![]() ЃЈЭђШЫЃЉЃЌдйИљОнФъСфдк
ЃЈЭђШЫЃЉЃЌдйИљОнФъСфдк![]() Ыъ~
Ыъ~![]() ЫъжЎМфУПдТЪЙгУЙВЯэЕЅГЕдк
ЫъжЎМфУПдТЪЙгУЙВЯэЕЅГЕдк![]() ДЮжЎМфЕФга
ДЮжЎМфЕФга![]() ШЫЃЌеМзмГщШЁШЫЪ§ЕФ
ШЫЃЌеМзмГщШЁШЫЪ§ЕФ![]() ЃЌЕУФъСфдк
ЃЌЕУФъСфдк![]() Ыъ
Ыъ![]() ЫъжЎМфЃЌУПдТЪЙгУЙВЯэЕЅГЕдк
ЫъжЎМфЃЌУПдТЪЙгУЙВЯэЕЅГЕдк![]() ДЮжЎМфЕФШЫЪ§дМЮЊ
ДЮжЎМфЕФШЫЪ§дМЮЊ![]() ЭђШЫ.
ЭђШЫ.
ЪдЬтНтЮіЃКНтЃКЃЈЂёЃЉ
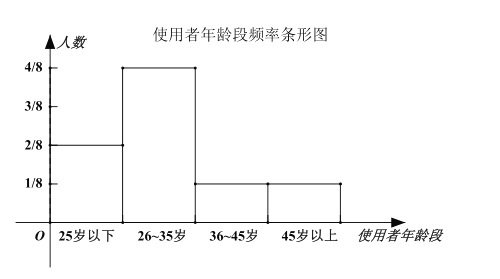
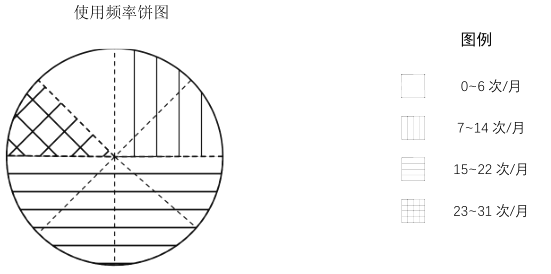

ЃЈЂђЃЉгЩБэЃЈЂёЃЉПЩжЊЃКФъСфдк![]() Ыъ~
Ыъ~![]() ЫъжЎМфЕФга
ЫъжЎМфЕФга![]() ШЫЃЌеМзмГщШЁШЫЪ§дквЛАыЃЌ
ШЫЃЌеМзмГщШЁШЫЪ§дквЛАыЃЌ
гУбљБОЙРМЦзмЬхЕФЫМЯыПЩжЊЃЌ
ФГГЧЧј![]() ЭђШЫПкжаФъСфдк
ЭђШЫПкжаФъСфдк![]() Ыъ~
Ыъ~![]() ЫъжЎМфЕФдМга
ЫъжЎМфЕФдМга![]() ЃЈЭђШЫЃЉЃК
ЃЈЭђШЫЃЉЃК
гжФъСфдк![]() Ыъ~
Ыъ~![]() ЫъжЎМфУПдТЪЙгУЙВЯэЕЅГЕдк
ЫъжЎМфУПдТЪЙгУЙВЯэЕЅГЕдк![]() ДЮжЎМфЕФга
ДЮжЎМфЕФга![]() ШЫЃЌеМзмГщШЁШЫЪ§ЕФ
ШЫЃЌеМзмГщШЁШЫЪ§ЕФ![]() ЃЌ
ЃЌ
гУбљБОЙРМЦзмЬхЕФЫМЯыПЩжЊЃЌГЧЧјФъСфдк![]() Ыъ
Ыъ![]() ЫъжЎМф
ЫъжЎМф![]() ЭђШЫжаУПдТЪЙгУЙВЯэЕЅГЕдк
ЭђШЫжаУПдТЪЙгУЙВЯэЕЅГЕдк![]() ДЮжЎМфЕФдМга
ДЮжЎМфЕФдМга![]() ЃЈЭђШЫЃЉ
ЃЈЭђШЫЃЉ
ЫљвдФъСфдк![]() Ыъ
Ыъ![]() ЫъжЎМфЃЌУПдТЪЙгУЙВЯэЕЅГЕдк
ЫъжЎМфЃЌУПдТЪЙгУЙВЯэЕЅГЕдк![]() ДЮжЎМфЕФШЫЪ§дМЮЊ
ДЮжЎМфЕФШЫЪ§дМЮЊ![]() ЭђШЫ
ЭђШЫ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ= ![]() Љ
Љ ![]() ЃЌ
ЃЌ
ЃЈ1ЃЉЧѓКЏЪ§fЃЈxЃЉЕФЖЈвхгђЃЛ
ЃЈ2ЃЉЧѓfЃЈЉ1ЃЉЃЌfЃЈ12ЃЉЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшaЃО0ЃЌ ![]() ЪЧRЩЯЕФХМКЏЪ§ЃЎ
ЪЧRЩЯЕФХМКЏЪ§ЃЎ
ЃЈ1ЃЉЧѓaЕФжЕЃЛ
ЃЈ2ЃЉжЄУїЃКfЃЈxЃЉдкЃЈ0ЃЌ+ЁоЃЉЩЯЪЧдіКЏЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЕиЗНеўИЎзМБИдквЛПщУцЛ§зуЙЛДѓЕФЛФЕиЩЯНЈвЛШчЭМЫљЪОЕФвЛИіОиаЮзлКЯаданЯаЙуГЁЃЌЦфзмУцЛ§ЮЊ3000ЦНЗНУзЃЌЦфжаГЁЕиЫФжмЃЈвѕгАВПЗжЃЉЮЊЭЈЕРЃЌЭЈЕРПэЖШОљЮЊ2УзЃЌжаМфЕФШ§ИіОиаЮЧјгђНЋЦЬЩшЫмНКЕиУцзїЮЊдЫЖЏГЁЕиЃЈЦфжаСНИіаЁГЁЕиаЮзДЯрЭЌЃЉЃЌЫмНКдЫЖЏГЁЕиеМЕиУцЛ§ЮЊSЦНЗНУзЃЎ 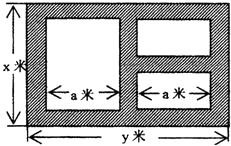
ЃЈ1ЃЉЗжБ№аДГігУxБэЪОyКЭSЕФКЏЪ§ЙиЯЕЪНЃЈаДГіКЏЪ§ЖЈвхгђЃЉЃЛ
ЃЈ2ЃЉдѕбљЩшМЦФмЪЙSШЁЕУзюДѓжЕЃЌзюДѓжЕЮЊЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊЬсИпЪаГЁЯњЪлвЕМЈЃЌФГЙЋЫОЩшМЦСНЬзВњЦЗДйЯњЗНАИЃЈЗНАИ1дЫзїЗбгУЮЊ![]() дЊ/МўЃЛЗНАИ2ЕФЕФдЫзїЗбгУЮЊ
дЊ/МўЃЛЗНАИ2ЕФЕФдЫзїЗбгУЮЊ![]() дЊ/МўЃЉЃЌВЂдкФГЕиЧјВПЗжгЊЯњЭјЕуНјааЪдЕуЃЈУПИіЪдЕуЭјЕужЛВЩгУвЛжжДйЯњЗНАИЃЉЃЌдЫзївЛФъКѓЃЌЖдБШИУЕиЧјЩЯвЛФъЖШЕФЯњЪлЧщПіЃЌЗжБ№ЭГМЦЯргІгЊЯњЭјЕуИіЪ§ЃЌжЦзїЯргІЕФСаСЊБэШчЯТБэЫљЪОЃЎ
дЊ/МўЃЉЃЌВЂдкФГЕиЧјВПЗжгЊЯњЭјЕуНјааЪдЕуЃЈУПИіЪдЕуЭјЕужЛВЩгУвЛжжДйЯњЗНАИЃЉЃЌдЫзївЛФъКѓЃЌЖдБШИУЕиЧјЩЯвЛФъЖШЕФЯњЪлЧщПіЃЌЗжБ№ЭГМЦЯргІгЊЯњЭјЕуИіЪ§ЃЌжЦзїЯргІЕФСаСЊБэШчЯТБэЫљЪОЃЎ
ЮоДйЯњЛюЖЏ | ВЩгУДйЯњЗНАИ1 | ВЩгУДйЯњЗНАИ2 | ||
БОФъЖШЦНОљЯњЪлЖюВЛИпгкЩЯвЛФъЖШЦНОљЯњЪлЖю | 48 | 11 | 31 | 90 |
БОФъЖШЦНОљЯњЪлЖюИпгкЩЯвЛФъЖШЦНОљЯњЪлЖю | 52 | 69 | 29 | 150 |
100 | 80 | 60 |
ЃЈЂёЃЉЧыИљОнСаСЊБэЬсЙЉЕФаХЯЂЃЌЮЊИУЙЋЫОНёФъбЁдёвЛЬзНЯЮЊгаРћЕФДйЯњЗНАИЃЈВЛБиЫЕУїРэгЩЃЉЃЛ
ЃЈЂђЃЉвбжЊИУЙЋЫОВњЦЗЕФГЩБОЮЊ10дЊ/МўЃЈЮДАќРЈДйЯњЛюЖЏдЫзїЗбгУЃЉЃЌЮЊжЦЖЈБОФъЖШИУЕиЧјЕФВњЦЗЯњЪлМлИёЃЌЭГМЦЩЯвЛФъЖШЕФ![]() зщЪлМл
зщЪлМл![]() ЃЈЕЅЮЛЃКдЊ/МўЃЌећЪ§ЃЉКЭЯњСП
ЃЈЕЅЮЛЃКдЊ/МўЃЌећЪ§ЃЉКЭЯњСП![]() ЃЈЕЅЮЛЃКМўЃЉЃЈ
ЃЈЕЅЮЛЃКМўЃЉЃЈ![]() ЃЉШчЯТБэЫљЪОЃК
ЃЉШчЯТБэЫљЪОЃК
ЪлМл |
|
|
|
|
|
|
|
|
ЯњСП |
|
|
|
|
|
|
|
|
ЃЈЂЁЃЉЧыИљОнЯТСаЪ§ОнМЦЫуЯргІЕФЯрЙижИЪ§![]() ЃЌВЂИљОнМЦЫуНсЙћЃЌбЁдёКЯЪЪЕФЛиЙщФЃаЭНјааФтКЯЃЛ
ЃЌВЂИљОнМЦЫуНсЙћЃЌбЁдёКЯЪЪЕФЛиЙщФЃаЭНјааФтКЯЃЛ
ЃЈЂЂЃЉИљОнЫљбЁЛиЙщФЃаЭЃЌЗжЮіЪлМл![]() ЖЈЮЊЖрЩйЪБЃПРћШѓ
ЖЈЮЊЖрЩйЪБЃПРћШѓ![]() ПЩвдДяЕНзюДѓЃЎ
ПЩвдДяЕНзюДѓЃЎ
|
|
| |
|
|
|
|
|
| ||
ВЮПМЙЋЪНЃКЯрЙижИЪ§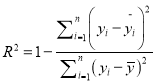 ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаУќЬтЕФЫЕЗЈДэЮѓЕФЪЧЃЈ ЃЉ
A.УќЬтЁАШєx2Љ3x+2=0ЃЌдђ x=1ЁБЕФФцЗёУќЬтЮЊЃКЁАШєxЁй1ЃЌдђx2Љ3x+2Ёй0ЁБЃЎ
B.ЁАx=1ЁБЪЧЁАx2Љ3x+2=0ЁБЕФГфЗжБивЊЬѕМўЃЎ
C.УќЬтpЃКЁА?xЁЪRЃЌsinx+cosxЁм ![]() ЁБЪЧецУќЬт
ЁБЪЧецУќЬт
D.ШєЉVЃЈpЁФqЃЉЮЊецУќЬтЃЌдђpЁЂqжСЩйгавЛИіЮЊМйУќЬтЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ ![]() гы
гы ![]() ЮЊЛЅЯрДЙжБЕФЕЅЮЛЯђСПЃЌ
ЮЊЛЅЯрДЙжБЕФЕЅЮЛЯђСПЃЌ ![]() ЃЌ
ЃЌ ![]() Чв
Чв ![]() гы
гы ![]() ЕФМаНЧЮЊШёНЧЃЌдђЪЕЪ§ІЫЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
ЕФМаНЧЮЊШёНЧЃЌдђЪЕЪ§ІЫЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
A.ЃЈЉЁоЃЌЉ2ЃЉ ![]()
B.ЃЈ ![]() ЃЌ+ЁоЃЉ
ЃЌ+ЁоЃЉ
C.ЃЈЉ2ЃЌ ![]() ЃЉ
ЃЉ ![]()
D.ЃЈЉ ![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§Са![]() КЭ
КЭ![]() Тњзу
Тњзу![]() Шє
Шє![]() ЮЊЕШБШЪ§СаЃЌЧв
ЮЊЕШБШЪ§СаЃЌЧв![]()
ЃЈ1ЃЉЧѓ![]() КЭ
КЭ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЩш![]() ЃЌМЧЪ§Са
ЃЌМЧЪ§Са![]() ЕФЧА
ЕФЧА![]() ЯюКЭЮЊ
ЯюКЭЮЊ![]()
ЂйЧѓ![]() ЃЛ
ЃЛ
ЂкЧѓе§ећЪ§ kЃЌЪЙЕУЖдШЮвт![]() Ољга
Ољга![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁАЮЂаХдЫЖЏЁБвбГЩЮЊЕБЯТШШУХЕФНЁЩэЗНЪНЃЌаЁЭѕЕФЮЂаХХѓгбШІФквВгаДѓСПКУгбВЮгыСЫЁАЮЂаХдЫЖЏЁБЃЌЫћЫцЛњбЁШЁСЫЦфжаЕФ40ШЫЃЈФаЁЂХЎИї20ШЫЃЉЃЌМЧТМСЫЫћУЧФГвЛЬьЕФзпТЗВНЪ§ЃЌВЂНЋЪ§ОнећРэШчЯТЃК
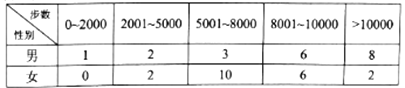
ЃЈ1ЃЉШєВЩгУбљБОЙРМЦзмЬхЕФЗНЪНЃЌЪдЙРМЦаЁЭѕЕФЫљгаЮЂаХКУгбжаУПШезпТЗВНЪ§ГЌЙ§5000ВНЕФИХТЪЃЛ
ЃЈ2ЃЉвбжЊФГШЫвЛЬьЕФзпТЗВНЪ§ГЌЙ§8000ВНБЛЯЕЭГЦРЖЈЁАЛ§МЋаЭЁБЃЌЗёдђЮЊЁАаИЕЁаЭЁБЃЌИљОнЬтвтЭъГЩЯТУцЕФ![]() СаСЊБэЃЌВЂОнДЫХаЖЯФмЗёга95%вдЩЯЕФАбЮеШЯЮЊЁАЦРЖЈРраЭЁБгыЁАадБ№ЁБгаЙиЃП
СаСЊБэЃЌВЂОнДЫХаЖЯФмЗёга95%вдЩЯЕФАбЮеШЯЮЊЁАЦРЖЈРраЭЁБгыЁАадБ№ЁБгаЙиЃП
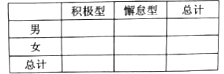 ИНЃК
ИНЃК 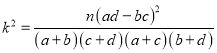 ЃЌ
ЃЌ
| 0ЃЎ10 | 0ЃЎ05 | 0ЃЎ025 | 0ЃЎ010 |
| 2ЃЎ706 | 3ЃЎ841 | 5ЃЎ024 | 6ЃЎ635 |
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com