
如图,三棱柱ABC-A1B1C1的侧面A1ACC1与底面ABC垂直,AB=BC=CA=4,且AA1⊥A1C,AA1=A1C. 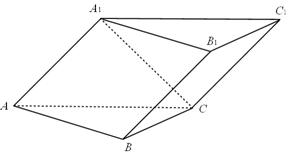
(Ⅰ)求侧棱AA1与底面ABC所成角的大小;
(Ⅱ)求侧面A1ABB1与底面ABC所成二面角的大小;
(Ⅲ)求顶点C到侧面A1ABB1的距离.
同下
解:(Ⅰ)作A1O⊥AC,垂足为O, ………1分
∵平面A1ACC1⊥平面ABC,∴ A1O⊥面ABC, ……2分
∴∠A1AO为A1A与面ABC所成的角. ……3分
∵AA1⊥A1C,AA1=A1C,∴∠A1AO=45°为所求. ……4分
(Ⅱ)以OB为x轴,OC为y轴,O A1为z轴建立空间直角坐标系,如图,
则![]() ,
,![]() ,
,![]() ,
,![]() .…5分
.…5分
设![]() 是面A1ACC1的法向量,则
是面A1ACC1的法向量,则![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,

∴ ,可取
,可取![]() . ……7分
. ……7分
而面ABC的法向量为![]() ,∵
,∵ ,…8分
,…8分
∴侧面A1ABB1与底面ABC所成二面角为![]() . ……9分
. ……9分
(Ⅲ)∵![]() ,∴
,∴![]() 在平面A1ACC1的法向量
在平面A1ACC1的法向量![]() 上的射影为
上的射影为
 , …………11分
, …………11分
∴点C到侧面A1ABB1的距离为![]() . ………12分
. ………12分


科目:高中数学 来源: 题型:
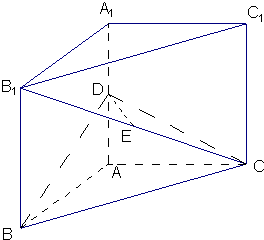 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC.查看答案和解析>>
科目:高中数学 来源: 题型:
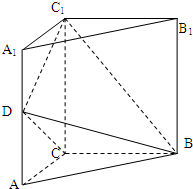 (2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=
(2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
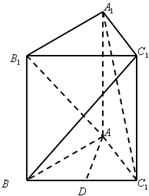 如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB
如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB查看答案和解析>>
科目:高中数学 来源: 题型:
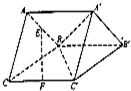 (2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=
(2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=| 2 |
| 2 |
| 2 |
| ||
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com