
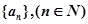 满足
满足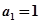 ,且对任意非负整数
,且对任意非负整数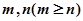 均有:
均有: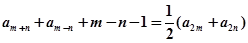 .
.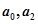 ;
;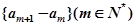 是等差数列,并求
是等差数列,并求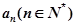 的通项;
的通项;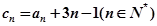 ,求证:
,求证: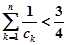 .
. 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
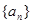 满足
满足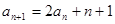 (
(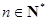 ).
).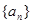 是等差数列,求它的首项和公差;
是等差数列,求它的首项和公差;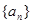 不可能是等比数列;
不可能是等比数列;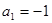 ,
,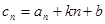 (
(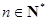 ),试求实数
),试求实数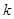 和
和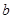 的值,使得数列
的值,使得数列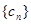 为等比数列;并求此时数列
为等比数列;并求此时数列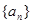 的通项公式.
的通项公式.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
|
2010年,我国南方省市遭遇旱涝灾害,为防洪抗旱,某地区大面积植树造林,如图,在区域 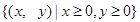 内植树,第一棵树在 内植树,第一棵树在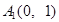 点,第二棵树在 点,第二棵树在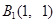 点,第三棵树在 点,第三棵树在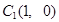 点,第四棵树在 点,第四棵树在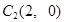 点,接着按图中箭头方向,每隔一个单位种一颗树,那么,第2014棵树所在的点的坐标是( ) 点,接着按图中箭头方向,每隔一个单位种一颗树,那么,第2014棵树所在的点的坐标是( )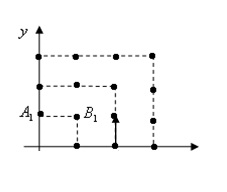
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com