
ЎѕМвДїЎїДіРЎРНЖуТµјЧІъЖ·ЙъІъµДН¶ИліЙ±ѕ![]() ЈЁµҐО»ЈєНтФЄЈ©УлІъЖ·ПъКЫКХИл
ЈЁµҐО»ЈєНтФЄЈ©УлІъЖ·ПъКЫКХИл![]() ЈЁµҐО»ЈєНтФЄЈ©ґжФЪЅПєГµДПЯРФ№ШПµЈ¬ПВ±нјЗВјБЛЧоЅь5ґОІъЖ·µДПа№ШКэѕЭ.
ЈЁµҐО»ЈєНтФЄЈ©ґжФЪЅПєГµДПЯРФ№ШПµЈ¬ПВ±нјЗВјБЛЧоЅь5ґОІъЖ·µДПа№ШКэѕЭ.
| 7 | 10 | 11 | 15 | 17 |
| 19 | 22 | 25 | 30 | 34 |
ЈЁ1Ј©Зу![]() №ШУЪ
№ШУЪ![]() µДПЯРФ»Ш№й·ЅіМЈ»
µДПЯРФ»Ш№й·ЅіМЈ»
ЈЁ2Ј©ёщѕЭЈЁ1Ј©ЦРµД»Ш№й·ЅіМЈ¬ЕР¶ПёГЖуТµјЧІъЖ·Н¶ИліЙ±ѕ20НтФЄµДГ«АыВКёьґу»№КЗН¶ИліЙ±ѕ24НтФЄµДГ«АыВКёьґуЈЁ![]() Ј©Јї
Ј©Јї
Па№Ш№«КЅЈє 
 Ј¬
Ј¬ ![]() .
.
Ўѕґр°ёЎїЈЁ1Ј©![]() .ЈЁ2Ј©Н¶ИліЙ±ѕ20НтФЄµДГ«АыВКёьґу.
.ЈЁ2Ј©Н¶ИліЙ±ѕ20НтФЄµДГ«АыВКёьґу.
ЎѕЅвОцЎїКФМв·ЦОцЈєЈЁ1Ј©Уɻع鹫ʽЈ¬ЅвµГПЯРФ»Ш№й·ЅіМОЄ![]() Ј»ЈЁ2Ј©µ±
Ј»ЈЁ2Ј©µ±![]() К±Ј¬
К±Ј¬ ![]() Ј¬¶ФУ¦µДГ«АыВКОЄ
Ј¬¶ФУ¦µДГ«АыВКОЄ![]() Ј¬µ±
Ј¬µ±![]() К±Ј¬
К±Ј¬ ![]() Ј¬¶ФУ¦µДГ«АыВКОЄ
Ј¬¶ФУ¦µДГ«АыВКОЄ![]() Ј¬№КН¶ИліЙ±ѕ20НтФЄµДГ«АыВКёьґуЎЈ
Ј¬№КН¶ИліЙ±ѕ20НтФЄµДГ«АыВКёьґуЎЈ
КФМвЅвОцЈє
ЈЁ1Ј©![]() Ј¬
Ј¬ ![]() Ј¬
Ј¬

![]() Ј¬
Ј¬ ![]() Ј¬№К
Ј¬№К![]() №ШУЪ
№ШУЪ![]() µДПЯРФ»Ш№й·ЅіМОЄ
µДПЯРФ»Ш№й·ЅіМОЄ![]() .
.
ЈЁ2Ј©µ±![]() К±Ј¬
К±Ј¬ ![]() Ј¬¶ФУ¦µДГ«АыВКОЄ
Ј¬¶ФУ¦µДГ«АыВКОЄ![]() Ј¬
Ј¬
µ±![]() К±Ј¬
К±Ј¬ ![]() Ј¬¶ФУ¦µДГ«АыВКОЄ
Ј¬¶ФУ¦µДГ«АыВКОЄ![]() Ј¬
Ј¬
№КН¶ИліЙ±ѕ20НтФЄµДГ«АыВКёьґу.
ЎѕМвРНЎїЅвґрМв
ЎѕЅбКшЎї
21
ЎѕМвДїЎїИзНјЈ¬ФЪХэ·ЅМе![]() ЦРЈ¬
ЦРЈ¬ ![]() ·Ц±рКЗАв
·Ц±рКЗАв![]() µДЦРµгЈ¬
µДЦРµгЈ¬ ![]() ОЄАв
ОЄАв![]() ЙПТ»µгЈ¬ЗТТмГжЦ±ПЯ
ЙПТ»µгЈ¬ЗТТмГжЦ±ПЯ![]() Ул
Ул![]() ЛщіЙЅЗµДУаПТЦµОЄ
ЛщіЙЅЗµДУаПТЦµОЄ![]() .
.

ЈЁ1Ј©Ц¤ГчЈє ![]() ОЄ
ОЄ![]() µДЦРµгЈ»
µДЦРµгЈ»
ЈЁ2Ј©ЗуЖЅГж![]() УлЖЅГж
УлЖЅГж![]() ЛщіЙИс¶юГжЅЗµДУаПТЦµ.
ЛщіЙИс¶юГжЅЗµДУаПТЦµ.
Ўѕґр°ёЎїЈЁ1Ј©јыЅвОцЈЁ2Ј©![]()
ЎѕЅвОцЎїКФМв·ЦОцЈєЈЁ1Ј©ТФ![]() ОЄЧш±кФµгЈ¬ЅЁБўИзНјЛщКѕµДїХјдЦ±ЅЗЧш±кПµ
ОЄЧш±кФµгЈ¬ЅЁБўИзНјЛщКѕµДїХјдЦ±ЅЗЧш±кПµ![]() Ј¬І»·ББоХэ·ЅМеµДАві¤ОЄ2Ј¬Йи
Ј¬І»·ББоХэ·ЅМеµДАві¤ОЄ2Ј¬Йи![]() Ј¬АыУГ
Ј¬АыУГ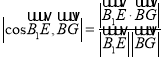 Ј¬ЅвµГ
Ј¬ЅвµГ![]() Ј¬јґїЙЦ¤µГЈ»
Ј¬јґїЙЦ¤µГЈ»
ЈЁ2Ј©·Ц±рЗуµГЖЅГж![]() УлЖЅГж
УлЖЅГж![]() µД·ЁПтБї
µД·ЁПтБї![]() Ј¬АыУГ
Ј¬АыУГ![]() ЗуЅвјґїЙ.
ЗуЅвјґїЙ.
КФМвЅвОцЈє
ЈЁ1Ј©Ц¤ГчЈєТФ![]() ОЄЧш±кФµгЈ¬ЅЁБўИзНјЛщКѕµДїХјдЦ±ЅЗЧш±кПµ
ОЄЧш±кФµгЈ¬ЅЁБўИзНјЛщКѕµДїХјдЦ±ЅЗЧш±кПµ![]() .
.
І»·ББоХэ·ЅМеµДАві¤ОЄ2Ј¬
Фт![]() Ј¬
Ј¬ ![]() Ј¬
Ј¬ ![]() Ј¬
Ј¬ ![]() Ј¬
Ј¬ ![]() Ј¬
Ј¬
Йи![]() Ј¬Фт
Ј¬Фт![]() Ј¬
Ј¬ ![]() Ј¬
Ј¬
ЛщТФ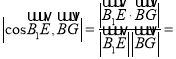
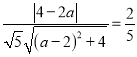 Ј¬
Ј¬
ЛщТФ![]() Ј¬ЅвµГ
Ј¬ЅвµГ![]() ЈЁ
ЈЁ![]() ЙбИҐЈ©Ј¬јґ
ЙбИҐЈ©Ј¬јґ![]() ОЄ
ОЄ![]() µДЦРµг.
µДЦРµг.
ЈЁ2Ј©ЅвЈєУЙЈЁ1Ј©їЙµГ![]() Ј¬
Ј¬ ![]() Ј¬
Ј¬
Йи![]() КЗЖЅГж
КЗЖЅГж![]() µД·ЁПтБїЈ¬
µД·ЁПтБїЈ¬
Фт![]() .Бо
.Бо![]() Ј¬µГ
Ј¬µГ![]() .
.
ТЧµГЖЅГж![]() µДТ»ёц·ЁПтБїОЄ
µДТ»ёц·ЁПтБїОЄ![]() Ј¬
Ј¬
ЛщТФ .
.
ЛщТФЛщЗуИс¶юГжЅЗµДУаПТЦµОЄ![]() .
.


 МмМмПтЙПТ»±ѕєГѕнПµБРґр°ё
МмМмПтЙПТ»±ѕєГѕнПµБРґр°ё РЎС§Йъ10·ЦЦУУ¦УГМвПµБРґр°ё
РЎС§Йъ10·ЦЦУУ¦УГМвПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїДіПХЦЦµД»щ±ѕ±Ј·СОЄa(µҐО»ЈєФЄ)Ј¬јМРш№єВтёГПХЦЦµДН¶±ЈИЛіЖОЄРш±ЈИЛЈ¬Рш±ЈИЛ±ѕДк¶ИµД±Ј·СУлЖдЙПДк¶ИіцПХґОКэµД№ШБЄИзПВЈє
ЙПДк¶ИіцПХґОКэ | 0 | 1 | 2 | 3 | 4 | ЎЭ5 |
±Ј·С | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
Лж»ъµчІйБЛёГПХЦЦµД200ГыРш±ЈИЛФЪТ»ДкДЪµДіцПХЗйїцЈ¬µГµЅИзПВНіјЖ±нЈє
іцПХґОКэ | 0 | 1 | 2 | 3 | 4 | ЎЭ5 |
ЖµКэ | 60 | 50 | 30 | 30 | 20 | 10 |
(1)јЗAОЄКВјюЈєЎ°Т»Рш±ЈИЛ±ѕДк¶ИµД±Ј·СІ»ёЯУЪ»щ±ѕ±Ј·СЎ±Ј¬ЗуP(A)µД№АјЖЦµЈ»
(2)јЗBОЄКВјюЈєЎ°Т»Рш±ЈИЛ±ѕДк¶ИµД±Ј·СёЯУЪ»щ±ѕ±Ј·Сµ«І»ёЯУЪ»щ±ѕ±Ј·СµД160%Ў±Ј¬ЗуP(B)µД№АјЖЦµЈ»
(3)ЗуРш±ЈИЛ±ѕДк¶ИЖЅѕщ±Ј·СµД№АјЖЦµЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
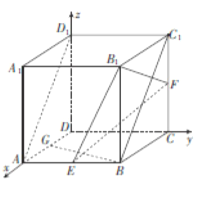
ЎѕМвДїЎїИзНј, ТСЦЄЛД±ЯРОABCDєНBCEGѕщОЄЦ±ЅЗМЭРОЈ¬ADЎОBC,CEЎОBGЈ¬ЗТ![]() Ј¬ЖЅГжABCDЎНЖЅГжBCEGЈ¬BC=CD=CE=2AD=2BG=2.
Ј¬ЖЅГжABCDЎНЖЅГжBCEGЈ¬BC=CD=CE=2AD=2BG=2.

ЈЁ1Ј©ЗуЦ¤:ECЎНCDЈ»
ЈЁ2Ј©ЗуЦ¤ЈєAGЎОЖЅГжBDEЈ»
ЈЁ3Ј©ЗуЈєјёєОМеEG-ABCDµДМе»э.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄєЇКэfЈЁxЈ©=2cos2¦Шx+ ![]() sin2¦ШxЈЁ¦ШЈѕ0Ј©µДЧоРЎХэЦЬЖЪОЄ¦РЈ¬ёшіцПВБРЛДёцГьМвЈє
sin2¦ШxЈЁ¦ШЈѕ0Ј©µДЧоРЎХэЦЬЖЪОЄ¦РЈ¬ёшіцПВБРЛДёцГьМвЈє
ўЩfЈЁxЈ©µДЧоґуЦµОЄ3Ј»
ўЪЅ«fЈЁxЈ©µДНјПуПтЧуЖЅТЖ ![]() єуЛщµГµДєЇКэКЗЕјєЇКэЈ»
єуЛщµГµДєЇКэКЗЕјєЇКэЈ»
ўЫfЈЁxЈ©ФЪЗшјд[©Ѓ ![]() Ј¬
Ј¬ ![]() ]ЙПµҐµчµЭФцЈ»
]ЙПµҐµчµЭФцЈ»
ўЬfЈЁxЈ©µДНјПу№ШУЪЦ±ПЯx= ![]() ¶ФіЖЈ®
¶ФіЖЈ®
ЖдЦРХэИ·Лµ·ЁµДРтєЕКЗЈЁ Ј©
A.ўЪўЫ
B.ўЩўЬ
C.ўЩўЪўЬ
D.ўЩўЫўЬ
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄєЇКэ![]() Ј¬
Ј¬![]() ЎЈ
ЎЈ
ўс.ЗуєЇКэ![]() µДЧоРЎХэЦЬЖЪєНµҐµчµЭФцЗшјдЈ»
µДЧоРЎХэЦЬЖЪєНµҐµчµЭФцЗшјдЈ»
ўт.µ±![]() К±Ј¬·ЅіМ
К±Ј¬·ЅіМ![]() ЗЎУРБЅёцІ»Н¬µДКµКэёщЈ¬ЗуКµКэ
ЗЎУРБЅёцІ»Н¬µДКµКэёщЈ¬ЗуКµКэ![]() µДИЎЦµ·¶О§Ј»
µДИЎЦµ·¶О§Ј»
ўу.Ѕ«єЇКэ![]() µДНјПуПтУТЖЅТЖ
µДНјПуПтУТЖЅТЖ![]() ёцµҐО»єуЛщµГєЇКэ
ёцµҐО»єуЛщµГєЇКэ![]() µДНјПу№ШУЪФµгЦРРД¶ФіЖЈ¬Зу
µДНјПу№ШУЪФµгЦРРД¶ФіЖЈ¬Зу![]() µДЧоРЎЦµЎЈ
µДЧоРЎЦµЎЈ
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄЖЅГжДЪµДПтБї![]() Ј¬
Ј¬![]() ВъЧгЈє
ВъЧгЈє![]() Ј¬
Ј¬![]() Ј¬ЗТ
Ј¬ЗТ![]() Ул
Ул![]() µДјРЅЗОЄ
µДјРЅЗОЄ![]() Ј¬УЦ
Ј¬УЦ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬ФтУЙВъЧгМхјюµДµг
Ј¬ФтУЙВъЧгМхјюµДµг![]() ЛщЧйіЙµДНјРОГж»эКЗЈЁ Ј©
ЛщЧйіЙµДНјРОГж»эКЗЈЁ Ј©
A. 2 B. ![]() C. 1 D.
C. 1 D. ![]()
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЙиєЇКэf(x)µД¶ЁТеУтОЄRЈ¬ІўЗТНјПу№ШУЪyЦб¶ФіЖЈ¬µ±xЎЬЈ1К±Ј¬yЈЅf(x)µДНјПуКЗѕ№эµг(Ј2,0)Ул(Ј1,1)µДЙдПЯЈ¬УЦФЪyЈЅf(x)µДНјПуЦРУРТ»Ії·ЦКЗ¶ҐµгФЪ(0,2)Ј¬ЗТѕ№эµг(1,1)µДТ»¶ОЕЧОпПЯЈ®
(1)КФЗуіцєЇКэf(x)µД±нґпКЅЈ¬ЧчіцЖдНјПуЈ»
(2)ёщѕЭНјПуЛµіцєЇКэµДµҐµчЗшјдЈ¬ТФј°ФЪГїТ»ёцµҐµчЗшјдЙПєЇКэКЗФцєЇКэ»№КЗјхєЇКэЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЙиєЇКэf(x)ЈЅ![]() ax2Ј1ЈlnxЈ¬ЖдЦРaЎКRЈ®
ax2Ј1ЈlnxЈ¬ЖдЦРaЎКRЈ®
ЈЁ1Ј©ИфaЈЅ0Ј¬Зу№эµг(0Ј¬Ј1)ЗТУлЗъПЯyЈЅf(x)ПаЗРµДЦ±ПЯ·ЅіМЈ»
ЈЁ2Ј©ИфєЇКэf(x)УРБЅёцБгµгx1Ј¬x2Ј¬
ўЩ ЗуaµДИЎЦµ·¶О§Ј»
ўЪ ЗуЦ¤Јєf Ўд(x1)Ј«f Ўд(x2)Јј0Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїјЧТТБЅµШПаѕа![]() Ј¬»хіµґУјЧµШФИЛЩРРК»µЅТТµШЈ¬ЛЩ¶ИІ»µГі¬№э
Ј¬»хіµґУјЧµШФИЛЩРРК»µЅТТµШЈ¬ЛЩ¶ИІ»µГі¬№э![]() Ј¬ТСЦЄ»хіµГїРЎК±µДФЛКдіЙ±ѕЈЁµҐО»ЈєФІЈ©УЙїЙ±д±ѕєН№М¶ЁЧйіЙЧйіЙЈ¬їЙ±діЙ±ѕКЗЛЩ¶ИЖЅ·ЅµД
Ј¬ТСЦЄ»хіµГїРЎК±µДФЛКдіЙ±ѕЈЁµҐО»ЈєФІЈ©УЙїЙ±д±ѕєН№М¶ЁЧйіЙЧйіЙЈ¬їЙ±діЙ±ѕКЗЛЩ¶ИЖЅ·ЅµД![]() ±¶Ј¬№М¶ЁіЙ±ѕОЄ
±¶Ј¬№М¶ЁіЙ±ѕОЄ![]() ФЄ.
ФЄ.
ЈЁ1Ј©Ѕ«И«іМФИЛЩФИЛЩіЙ±ѕ![]() ЈЁФЄЈ©±нКѕОЄЛЩ¶И
ЈЁФЄЈ©±нКѕОЄЛЩ¶И![]() µДєЇКэЈ¬ІўЦёіцХвёцєЇКэµД¶ЁТеУтЈ»
µДєЇКэЈ¬ІўЦёіцХвёцєЇКэµД¶ЁТеУтЈ»
ЈЁ2Ј©Иф![]() Ј¬ОЄБЛК№И«іМФЛКдіЙ±ѕЧоРЎЈ¬»хіµУ¦ТФ¶аґуµДЛЩ¶ИРРК»Јї
Ј¬ОЄБЛК№И«іМФЛКдіЙ±ѕЧоРЎЈ¬»хіµУ¦ТФ¶аґуµДЛЩ¶ИРРК»Јї
Ійїґґр°ёєНЅвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com