
����Ŀ����֪����![]() ��ͼ����
��ͼ����![]() ����
����![]() �������������ľ���Ϊ
�������������ľ���Ϊ![]() ��Ϊ�õ�
��Ϊ�õ�![]() ��ͼ�ɽ�
��ͼ�ɽ�![]() ͼ�������е㣨 ��
ͼ�������е㣨 ��
A.������ƽ��![]() ����λ���ٽ�����ͼ�������е�ĺ���������Ϊԭ����
����λ���ٽ�����ͼ�������е�ĺ���������Ϊԭ����![]() �������겻��
�������겻��
B.������ƽ��![]() ����λ���ٽ�����ͼ�������е�ĺ���������Ϊԭ����
����λ���ٽ�����ͼ�������е�ĺ���������Ϊԭ����![]() �������겻��
�������겻��
C.������ƽ��![]() ����λ���ٽ�����ͼ�������е�ĺ������쳤Ϊԭ����2���������겻��
����λ���ٽ�����ͼ�������е�ĺ������쳤Ϊԭ����2���������겻��
D.������ƽ��![]() ����λ���ٽ�����ͼ�������е�ĺ������쳤Ϊԭ����2���������겻��
����λ���ٽ�����ͼ�������е�ĺ������쳤Ϊԭ����2���������겻��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
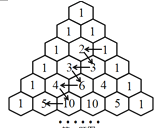
����Ŀ��������ǣ�������ʽϵ�����������е�һ�ּ������С���ŷ�ޣ������������˹������������˹����1623----1662������1654�귢����һ�����ģ������Ҫ��393�꣬��������600�ꡣ��ͼ�ı����ҹ�������ѧ�����1261�������ġ��������㷨��һ����ͳ����ˣ��������ҹ���ѧʷ�ϵ�һ��ΰ��ɾ͡���ͼ��ʾ���ڡ�������ǡ��У���1��ʼ��ͷ��ָ�������һ����������У�1,2,3,3,6,4,10,5�������������ǰ16���Ϊ�� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ȤС��������20�ˣ�Ů��10�ˣ����г�ȡһ������Ϊ5��������ǡ�ó鵽2��������3��Ů������
�ٸó���������ϵͳ������
�ڸó������������������
�۸ó���һ�����Ƿֲ������
�ܱ��γ�����ÿ���˱��鵽�ĸ��ʶ���![]() ��
��
����˵����ȷ��Ϊ�� ��
A.�٢ڢ�B.�ڢ�C.�ڢۢ�D.�ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�CΪֱ��y��5�ϵĶ��㣬��CΪԲ�ĵ�ԲC��y�����õ��ҳ���Ϊ6����ԭ��O��ԲC��һ�����ߣ��е�ΪP�����P��ֱ��3x+4y��25��0�ľ������СֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ľ��飬ij��������ʩ���ڼ�Ľ�ˮ��![]() ����λ��
����λ��![]() ���Թ��ڵ�Ӱ�����±���
���Թ��ڵ�Ӱ�����±���

����ij����վ�����ϣ�ij����С�鳭¼�˸ù���ʩ����ij��ǰ20��Ľ�ˮ�������ݣ����Ƶõ���ˮ��������ͼ������ͼ��ʾ.
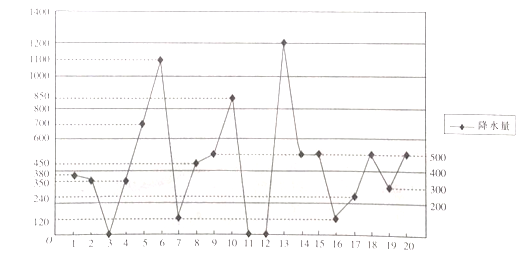
��1������20���ƽ����ˮ����
��2�����ݽ�ˮ��������ͼ���ֱ���Ƹù���ʩ����������![]() �ĸ���.
�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������A��BCD�У���ABC�͡�ABD������ABΪб�ߵ�ֱ�������Σ�AB��CD��AB��10��CD��6��
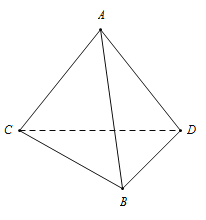
��1������AB���Ƿ���ڵ�E��ʹ��AB��ƽ��ECD��
��2�����S��ABC��S��ABD��30��������C��AB��D�Ĵ�С��
��3��������A��BCD��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1����ƽ��ֱ������ϵ�У�![]() �ķ���Ϊ
�ķ���Ϊ![]() ��
��![]() �ķ���Ϊ
�ķ���Ϊ![]() ����Բ�����ڵ�
����Բ�����ڵ�![]() ����Բ
����Բ![]() ��
��![]() ������
������![]() ����.
����.

��1����Բ![]() Բ��
Բ��![]() �Ĺ켣���̣�
�Ĺ켣���̣�
��2����ͼ��2������![]() ����
����![]() ����������
����������![]() ����Բ����ֱ��
����Բ����ֱ��![]() �ϵ�
�ϵ�![]() Ҳͬʱ��
Ҳͬʱ��![]() ���У����
���У����![]() Ϊ
Ϊ![]() ��һ��������Բ��
��һ��������Բ��

��������![]() ʱ����֤��
ʱ����֤��![]() �İ뾶Ϊ��ֵ��
�İ뾶Ϊ��ֵ��
�������ڣ������������£���֪![]() ����
����![]() ������
������![]() ������
���У���![]() ��Բ��Ϊ
��Բ��Ϊ![]() ����֤����
����֤����![]() �ġ�����Բ��
�ġ�����Բ��![]() ���У���
���У���![]() Ҳ���С�
Ҳ���С�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() ��ֱ��
��ֱ��![]() ����ֱ��
����ֱ��![]() ������
������![]() .
.
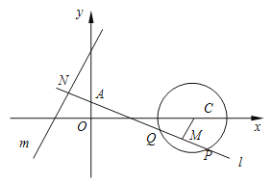
��1����ֱ��![]() ��Բ
��Բ![]() ���У���ֱ��
���У���ֱ��![]() �ķ��̣�
�ķ��̣�
��2����ֱ��![]() ��Բ
��Բ![]() �ཻ��
�ཻ��![]() ���㣬��
���㣬��![]() ��
��![]() ���е㣬ֱ��
���е㣬ֱ��![]() ��ֱ��
��ֱ��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() . ̽��
. ̽��![]() �Ƿ�Ϊ��ֵ�����ǣ�����ö�ֵ�������ǣ���˵������.
�Ƿ�Ϊ��ֵ�����ǣ�����ö�ֵ�������ǣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����й����걨��2015��5��14�ձ����������������缼�������չ�����ڵ����������˱�ըʽ��������2014���������۶�ﵽ��27898��Ԫ��ռ�������Ʒ�����ܶ��10%��Ҳ����˵�������ճ�������10%��ͨ�����������һ�����30%��40%���ٶ�����."����2014-2020���������۶�ÿ��������ʾ�Ϊ35%�������2015-2020��ÿ����������۶��ȷ��1��Ԫ��.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com