
【题目】已知函数f(x)=sin(2x+ ![]() ),f′(x)是f(x)的导函数,则函数y=2f(x)+f′(x)的一个单调递减区间是( )
),f′(x)是f(x)的导函数,则函数y=2f(x)+f′(x)的一个单调递减区间是( )
A.[ ![]() ,
, ![]() ]
]
B.[﹣ ![]() ,
, ![]() ]
]
C.[﹣ ![]() ,
, ![]() ]
]
D.[﹣ ![]() ,
, ![]() ]
]
【答案】A
【解析】解:函数f(x)=sin(2x+ ![]() ),f′(x)是f(x)的导函数, 则函数y=2f(x)+f′(x)=2sin(2x+
),f′(x)是f(x)的导函数, 则函数y=2f(x)+f′(x)=2sin(2x+ ![]() )+2cos(2x+
)+2cos(2x+ ![]() )
)
= ![]() sin(2x+
sin(2x+ ![]() +
+ ![]() )=2
)=2 ![]() sin(2x+
sin(2x+ ![]() ),
),
由2kπ+ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,
,k∈Z,
可得:kπ+ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,k∈Z,
,k∈Z,
所以函数的一个单调减区间为:[ ![]() ,
, ![]() ].
].
故选:A.
【考点精析】认真审题,首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减),还要掌握正弦函数的单调性(正弦函数的单调性:在
在这个区间单调递减),还要掌握正弦函数的单调性(正弦函数的单调性:在![]()
![]() 上是增函数;在
上是增函数;在![]()
![]() 上是减函数)的相关知识才是答题的关键.
上是减函数)的相关知识才是答题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的左、右焦点为F1 , F2 , 设点F1 , F2与椭圆短轴的一个端点构成斜边长为4的直角三角形.
=1(a>b>0)的左、右焦点为F1 , F2 , 设点F1 , F2与椭圆短轴的一个端点构成斜边长为4的直角三角形.
(1)求椭圆C的标准方程;
(2)设A,B,P为椭圆C上三点,满足 ![]() =
= ![]()
![]() +
+ ![]()
![]() ,记线段AB中点Q的轨迹为E,若直线l:y=x+1与轨迹E交于M,N两点,求|MN|.
,记线段AB中点Q的轨迹为E,若直线l:y=x+1与轨迹E交于M,N两点,求|MN|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ax+ ![]() ,且f(x)+f(
,且f(x)+f( ![]() )=0,其中a,b为常数.
)=0,其中a,b为常数.
(1)若函数f(x)的图象在x=1的切线经过点(2,5),求函数的解析式;
(2)已知0<a<1,求证:f( ![]() )>0;
)>0;
(3)当f(x)存在三个不同的零点时,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】非零向量 ![]() ,
, ![]() 的夹角为
的夹角为 ![]() ,且满足|
,且满足| ![]() |=λ|
|=λ| ![]() |(λ>0),向量组
|(λ>0),向量组 ![]() ,
, ![]() ,
, ![]() 由一个
由一个 ![]() 和两个
和两个 ![]() 排列而成,向量组
排列而成,向量组 ![]() ,
, ![]() ,
, ![]() 由两个
由两个 ![]() 和一个
和一个 ![]() 排列而成,若
排列而成,若 ![]()
![]() +
+ ![]()
![]() +
+ ![]()
![]() 所有可能值中的最小值为4
所有可能值中的最小值为4 ![]() 2 , 则λ= .
2 , 则λ= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x﹣1|﹣|2x+1|的最大值为m.
(Ⅰ)作出函数f(x)的图象;
(Ⅱ)若a2+2c2+3b2=m,求ab+2bc的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四菱锥P﹣ABCD中,PA⊥AD,PA=1,PC=PD,底面ABCD是梯形,AB∥CD,AB⊥BC,AB=BC=1,CD=2.
(I)求证:PA⊥AB;
(II)求直线AD与平面PCD所成角的大小.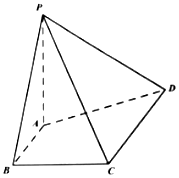
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com