
【题目】瑞士数学家、物理学家欧拉发现任一凸多面体(即多面体内任意两点的连线都被完全包含在该多面体中,直观上讲是指没有凹陷或孔洞的多面体)的顶点数V.棱数E及面数F满足等式![]() ,这个等式称为欧拉多面体公式,被认为是数学领域最漂亮、简洁的公式之一,现实生活中存在很多奇妙的几何体,现代足球的外观即取自一种不完全正多面体,它是由m块黑色正五边形面料和
,这个等式称为欧拉多面体公式,被认为是数学领域最漂亮、简洁的公式之一,现实生活中存在很多奇妙的几何体,现代足球的外观即取自一种不完全正多面体,它是由m块黑色正五边形面料和![]() 块白色正六边形面料构成的.则
块白色正六边形面料构成的.则![]() ( )
( )

A.20B.18C.14D.12
科目:高中数学 来源: 题型:
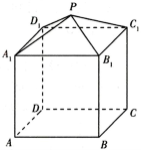
【题目】如图是一个由正四棱锥![]() 和正四棱柱
和正四棱柱![]() 构成的组合体,正四棱锥的侧棱长为6,
构成的组合体,正四棱锥的侧棱长为6,![]() 为正四棱锥高的4倍.当该组合体的体积最大时,点
为正四棱锥高的4倍.当该组合体的体积最大时,点![]() 到正四棱柱
到正四棱柱![]() 外接球表面的最小距离是( )
外接球表面的最小距离是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌布娃娃做促销活动:已知有50个布娃娃,其中一些布娃娃里面有奖品,参与者可以先在50个布娃娃中购买5个,看完5个布娃娃里面的结果再决定是否将剩下的布娃娃全部购买,设每个布娃娃有奖品的概率为![]() ,且各个布娃娃是否有奖品相互独立.
,且各个布娃娃是否有奖品相互独立.
(1)记5个布娃娃中有1个有奖品的概率为![]() ,当
,当![]() 时,
时,![]() 的最大值,求
的最大值,求![]() ;
;
(2)假如这5个布娃娃中恰有1个有奖品,以上问中的![]() 作为p的值.已知每次购买布娃娃需要2元,若有中奖,则中奖者每次可得奖金15元.以最终奖金的期望作为决策依据,是否该买下剩下所有的45个布娃娃;
作为p的值.已知每次购买布娃娃需要2元,若有中奖,则中奖者每次可得奖金15元.以最终奖金的期望作为决策依据,是否该买下剩下所有的45个布娃娃;
(3)若已知50件布娃娃中有10个布娃娃有奖品,从这堆布娃娃中任意购买5个,若抽到k个有奖品可能性最大,求k的值.(k为正整数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某玩具厂拟定生产两款新毛绒玩具样品,一款为毛绒小猪,另一款为毛绒小狗.由设计图知,生产这两款毛绒玩具均需相同材质的填充物、长毛绒、天鹅绒,且每个毛绒小猪需填充物![]() 、长毛绒
、长毛绒![]() 、天鹅绒
、天鹅绒![]() ,每个毛绒小狗需填充物
,每个毛绒小狗需填充物![]() 、长毛绒
、长毛绒![]() 、天鹅绒
、天鹅绒![]() .现有所需填充物
.现有所需填充物![]() 、长毛绒
、长毛绒![]() 、天鹅绒
、天鹅绒![]() ,若每个毛绒小猪与毛绒小狗的出厂价分别为64元、36元,则生这批毛绒玩具的最大销售额为_______元.
,若每个毛绒小猪与毛绒小狗的出厂价分别为64元、36元,则生这批毛绒玩具的最大销售额为_______元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知可导函数f(x)的定义域为![]() ,且满足
,且满足![]() ,
,![]() ,则对任意的
,则对任意的![]() ,“
,“![]() ”是“
”是“![]() ”的( )
”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱![]() 中,四边形ABCD为平行四边形,
中,四边形ABCD为平行四边形,![]() 且点
且点![]() 在底面上的投影H恰为CD的中点.
在底面上的投影H恰为CD的中点.
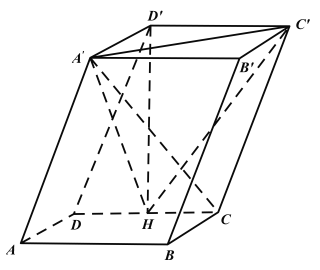
(1)棱BC上存在一点N,使得AD⊥平面![]() ,试确定点N的位置,说明理由;
,试确定点N的位置,说明理由;
(2)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有6名选手参加才艺比赛,其中男、女选手各3名,且3名男选手分别表演歌唱、舞蹈和魔术,3名女选手分别表演歌唱、舞蹈和魔术,若要求相邻出场的选手性别不同且表演的节目不同,则不同的出场方式的种数为( )
A.6B.12C.18D.24
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 在
在![]() 处取得极大值或极小值,则称
处取得极大值或极小值,则称![]() 为函数
为函数![]() 的极值点.设函数
的极值点.设函数![]() .
.
(1)若函数![]() 在
在![]() 上无极值点,求
上无极值点,求![]() 的取值范围;
的取值范围;
(2)求证:对任意实数![]() ,在函数
,在函数![]() 的图象上总存在两条切线相互平行;
的图象上总存在两条切线相互平行;
(3)当![]() 时,若函数
时,若函数![]() 的图象上存在的两条平行切线之间的距离为4,问;这样的平行切线共有几组?请说明理由.
的图象上存在的两条平行切线之间的距离为4,问;这样的平行切线共有几组?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com