
【题目】如图,O为坐标原点,椭圆C1: ![]() +
+ ![]() =1(a>b>0)的左、右焦点分别为F1 , F2 , 离心率为e1;双曲线C2:
=1(a>b>0)的左、右焦点分别为F1 , F2 , 离心率为e1;双曲线C2: ![]() ﹣
﹣ ![]() =1的左、右焦点分别为F3 , F4 , 离心率为e2 , 已知e1e2=
=1的左、右焦点分别为F3 , F4 , 离心率为e2 , 已知e1e2= ![]() ,且|F2F4|=
,且|F2F4|= ![]() ﹣1.
﹣1.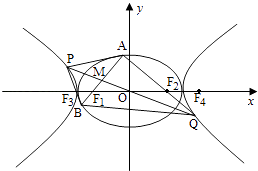
(Ⅰ)求C1、C2的方程;
(Ⅱ)过F1作C1的不垂直于y轴的弦AB,M为AB的中点,当直线OM与C2交于P,Q两点时,求四边形APBQ面积的最小值.
【答案】解:(Ⅰ)由题意可知, ![]() ,且
,且 ![]() .
.
∵e1e2= ![]() ,且|F2F4|=
,且|F2F4|= ![]() ﹣1.
﹣1.
∴ ![]() ,且
,且 ![]() .
.
解得: ![]() .
.
∴椭圆C1的方程为 ![]() ,双曲线C2的方程为
,双曲线C2的方程为 ![]() ;
;
(Ⅱ)由(Ⅰ)可得F1(﹣1,0).
∵直线AB不垂直于y轴,
∴设AB的方程为x=ny﹣1,
联立 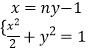 ,得(n2+2)y2﹣2ny﹣1=0.
,得(n2+2)y2﹣2ny﹣1=0.
设A(x1,y1),B(x2,y2),M(x0,y0),
则 ![]() ,
, ![]() .
.
则 ![]()
= ![]() =
= ![]() .
.
∵M在直线AB上,
∴ ![]() .
.
直线PQ的方程为 ![]() ,
,
联立 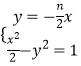 ,得
,得 ![]() .
.
解得 ![]() ,代入
,代入 ![]() 得
得 ![]() .
.
由2﹣n2>0,得﹣ ![]() <n<
<n< ![]() .
.
∴P,Q的坐标分别为 ![]() ,
,
则P,Q到AB的距离分别为: 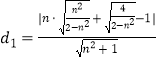 ,
, 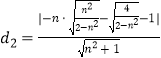 .
.
∵P,Q在直线A,B的两端,
∴ 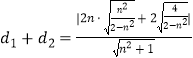 .
.
则四边形APBQ的面积S= ![]() |AB|
|AB| ![]() .
.
∴当n2=0,即n=0时,四边形APBQ面积取得最小值2
【解析】(1)利用已知条件即可求出a、b的值,从而可求出椭圆以及双曲线的标准方程;(2)设出直线的方程与椭圆的联立解出交点坐标,用未知数表示所求图形的面积,再利用未知数的取值范围即可求出所求图形面积的最小值。


 互动英语系列答案
互动英语系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:
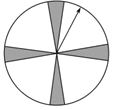
甲商场:顾客转动如图所示圆盘,当指针指向阴影部分(图中四个阴影部分均为扇形,且每个扇形圆心角均为![]() ,边界忽略不计)即为中奖.
,边界忽略不计)即为中奖.
乙商场:从装有3个白球3个红球的盒子中一次性摸出2个球(球除颜色外不加区分),如果摸到的是2个红球,即为中奖.问:购买该商品的顾客在哪家商场中奖的可能性大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1,a2=2,以后各项由an=an﹣1+an﹣2(n≥3)给出.
(1)写出此数列的前5项;
(2)通过公式bn= ![]() 构造一个新的数列{bn},写出数列{bn}的前4项.
构造一个新的数列{bn},写出数列{bn}的前4项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心在直线y=4x上,且与直线l:x+y﹣2=0相切于点P(1,1)
(Ⅰ)求圆的方程
(II)直线kx﹣y+3=0与该圆相交于A、B两点,若点M在圆上,且有向量 ![]() (O为坐标原点),求实数k.
(O为坐标原点),求实数k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】联合国教科文组织规定,每年的4月23日是“世界读书日”.某校研究生学习小组为了解本校学生的阅读情况,随机调查了本校400名学生在这一天的阅读时间![]() (单位:分钟),将时间数据分成5组:
(单位:分钟),将时间数据分成5组:![]() ,并整理得到如下频率分布直方图.
,并整理得到如下频率分布直方图.
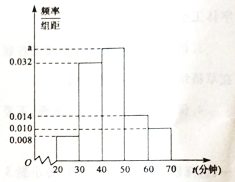
(1)求![]() 的值;
的值;
(2)试估计该学校所有学生在这一天的平均阅读时间;
(3)若用分层抽样的方法从这400名学生中抽取50人参加交流会,则在阅读时间为![]() 的两组中分别抽取多少人?
的两组中分别抽取多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com