
【题目】如图,在三棱锥P﹣ABC中,PC⊥平面ABC,∠PAC=30°,∠ACB=45°,BC=2 ![]() ,PA⊥AB.
,PA⊥AB. 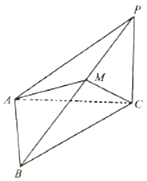
(1)求PC的长;
(2)若点M在侧棱PB上,且 ![]() ,当λ为何值时,二面角B﹣AC﹣M的大小为30°.
,当λ为何值时,二面角B﹣AC﹣M的大小为30°.
【答案】
(1)解:∵PC⊥平面ABC,PA⊥AB,∴AB⊥AC,
以A为原点,AB为x轴,AC为y轴,过A作平面ABC的垂线为z轴,建立空间直角坐标系,
∵PA⊥AB,∴ ![]() =0,
=0,
∴( ![]() )(
)( ![]() )=
)= ![]() =0,
=0,
∵PC⊥平面ABC,∴ ![]()
![]() =0,
=0, ![]() =0,
=0,
∴﹣| ![]() ||
|| ![]() |cos∠ACB+|
|cos∠ACB+| ![]() |2=0,
|2=0,
即﹣ ![]() ,
,
解得AC=2,
在Rt ![]() 中,PC=ACsin30°=
中,PC=ACsin30°= ![]()
(2)解:B(2,0,0),C(0,2,0),P(0,2, ![]() ),
),
∵点M在侧棱PB上,且 ![]() ,
,
∴M( ![]() ,
, ![]() ,
, ![]() ),
),
设平面ACM的一个法向量为 ![]() =(x,y,z),
=(x,y,z),
则 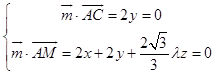 ,取z=1,得
,取z=1,得 ![]() =(﹣
=(﹣ ![]() ),
),
平面ABC的一个法向量 ![]() =(0,0,1),
=(0,0,1),
∵二面角B﹣AC﹣M的大小为30°,
∴cos30°= ![]() =
= 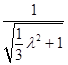 =
= ![]() =,
=,
解得λ=1或λ=﹣1(舍),
∴当λ=1时,二面角B﹣AC﹣M的大小为30°.
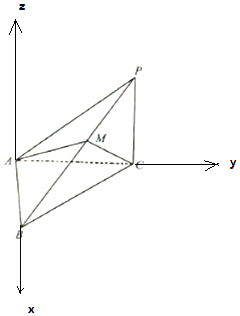
【解析】(1)以A为原点,AB为x轴,AC为y轴,过A作平面ABC的垂线为z轴,建立空间直角坐标系,利用向量法能求出PC.(2)求出平面ACM的一个法向量和平面ABC的一个法向量,利用向量法能求出当λ=1时,二面角B﹣AC﹣M的大小为30°.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
【题目】将函数y=sinx的图象经过下列哪种变换可以得到函数y=cos2x的图象( )
A.先向左平移 ![]() 个单位,然后再沿x轴将横坐标压缩到原来的
个单位,然后再沿x轴将横坐标压缩到原来的 ![]() 倍(纵坐标不变)
倍(纵坐标不变)
B.先向左平移 ![]() 个单位,然后再沿x轴将横坐标伸长到原来的2倍(纵坐标不变)
个单位,然后再沿x轴将横坐标伸长到原来的2倍(纵坐标不变)
C.先向左平移 ![]() 个单位,然后再沿x轴将横坐标压缩到原来的
个单位,然后再沿x轴将横坐标压缩到原来的 ![]() 倍(纵坐标不变)
倍(纵坐标不变)
D.先向左平移 ![]() 个单位,然后再沿x轴将横坐标伸长到原来的2倍(纵坐标不变)
个单位,然后再沿x轴将横坐标伸长到原来的2倍(纵坐标不变)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知六棱锥P﹣ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB则下列结论正确的是( ) 
A.PB⊥AD
B.平面PAB⊥平面PBC
C.直线BC∥平面PAE
D.直线PD与平面ABC所成的角为45°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,我艇在A处发现一走私船在方位角45°且距离为12海里的B处正以每小时10海里的速度向方位角105°的方向逃窜,我艇立即以14海里/小时的速度追击,求我艇追上走私船所需要的最短时间. 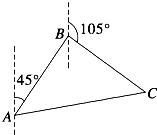
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不等式组 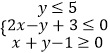 表示的平面区域为D,若(x,y)∈D,|x|+2y≤a为真命题,则实数a的取值范围是( )
表示的平面区域为D,若(x,y)∈D,|x|+2y≤a为真命题,则实数a的取值范围是( )
A.[10,+∞)
B.[11,+∞)
C.[13,+∞)
D.[14,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲、乙两煤矿每年的产量分别为200万吨和260万吨,需经过东车站和西车站两个车站运往外地.东车站每年最多能运280万吨煤,西车站毎年最多能运360万吨煤,甲煤矿运往东车站和西车站的运费价格分别为1元/t和1.5元/t,乙煤矿运往东车站和西车站的运费价格分别为0.8元/t和1.6元/t.煤矿应怎样编制调运方案,能使总运费最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的三个内角A、B、C所对的边分别为a、b、c,1+ ![]() =
= ![]() .
.
(1)求A的大小;
(2)若△ABC为锐角三角形,求函数y=2sin2B﹣2cosBcosC的取值范围;
(3)现在给出下列三个条件:①a=1;②2c﹣( ![]() +1)b=0;③B=45°,试从中再选择两个条件,以确定△ABC,求出所确定的△ABC的面积.
+1)b=0;③B=45°,试从中再选择两个条件,以确定△ABC,求出所确定的△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com