
在平面直角坐标系xOy中,椭圆C的中心为原点,焦点F1,F2在x轴上,离心率为 .过F1的直线交椭圆C于A,B两点,且△ABF2的周长为8.过定点M(0,3)的直线l1与椭圆C交于G,H两点(点G在点M,H之间).
.过F1的直线交椭圆C于A,B两点,且△ABF2的周长为8.过定点M(0,3)的直线l1与椭圆C交于G,H两点(点G在点M,H之间).
(1)求椭圆C的方程;
(2)设直线l1的斜率k>0,在x轴上是否存在点P(m,0),使得以PG,PH为邻边的平行四边形为菱形?如果存在,求出m的取值范围;如果不存在,请说明理由.
(1) 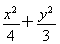 =1(2)
=1(2)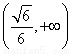
【解析】(1)设椭圆的方程为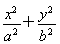 =1(a>b>0),由离心率e=
=1(a>b>0),由离心率e= =
=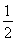 ,△ABF2的周长为|AF1|+|AF2|+|BF1|+|BF2|=4a=8,得a=2,c=1,则b2=a2-c2=3.
,△ABF2的周长为|AF1|+|AF2|+|BF1|+|BF2|=4a=8,得a=2,c=1,则b2=a2-c2=3.
所以椭圆C的方程为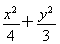 =1.
=1.
(2)由题意可知,直线l1的方程为y=kx+3(k>0).
由 得(3+4k2)x2+24kx+24=0,①
得(3+4k2)x2+24kx+24=0,①
Δ=(24k)2-4×24×(3+4k2)>0,解得k>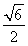 .
.
设椭圆的弦GH的中点为N(x0,y0),则“在x轴上是否存在点P(m,0),使得以PG,PH为邻边的平行四边形为菱形”等价于“在x轴上是否存在点P(m,0),使得PN⊥l1”.
设G(x1,y1),H(x2,y2),由韦达定理,得x1+x2=-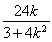 ,
,
则x0= =-
=-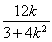 ,所以y0=kx0+3=
,所以y0=kx0+3=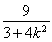 ,
,
即N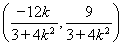 ,kPN=-
,kPN=-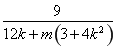 .
.
从而-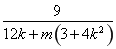 ·k=-1,
·k=-1,
解得m=-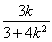
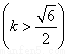 .
.
又因为m′(k)=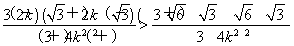 >0,
>0,
所以函数m=-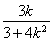 在定义域
在定义域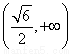 上单调递增,且mmin=m
上单调递增,且mmin=m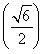 =-
=-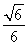 ,即m∈
,即m∈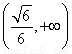 .
.
故存在满足条件的点P(m,0),m的取值范围为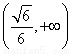


科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集3B讲练习卷(解析版) 题型:选择题
设奇函数f(x)在[-1,1]上是增函数,且f(-1)=-1,若函数f(x)≤t2-2at+1对所有的x∈[-1,1]都成立,则当a∈[-1,1]时t的取值范围是( )
A.-2≤t≤2 B.- ≤t≤
≤t≤
C.t≤-2或t=0或t≥2 D.t≤- 或t=0或t≥
或t=0或t≥
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集2A讲练习卷(解析版) 题型:选择题
已知向量a=(1,2),b=(1,0),c=(3,4),若λ为实数,且(b+λa)⊥c,则λ=( )
A.- B.-
B.- C.
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集1B讲练习卷(解析版) 题型:选择题
若复数 (a∈R,i是虚数单位)是纯虚数,则a的值为( )
(a∈R,i是虚数单位)是纯虚数,则a的值为( )
A.-2 B.2 C.1 D.-1
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集1A讲练习卷(解析版) 题型:选择题
设全集U=R,A={x|2x(x-2)<1},B={x|y=ln(1-x)},则A∩(∁RB)=( )
A.{x|x≥1} B.{x|1≤x<2}
C.{x|0<x≤1} D.{x|x≤1}
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集19讲练习卷(解析版) 题型:选择题
已知函数f(x)=x2-2(a+2)x+a2,g(x)=-x2+2(a-2)x-a2+8.设 H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)}(max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值),记H1(x)的最小值为A,H2(x)的最大值为B,则A-B=( )
A.a2-2a-16 B.a2+2a-16 C.-16 D.16
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集19讲练习卷(解析版) 题型:填空题
已知函数f(x)=asin 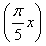 +btan
+btan  (a,b为常数),若f(1)=1,则不等式f(31)>log2x的解集为________.
(a,b为常数),若f(1)=1,则不等式f(31)>log2x的解集为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集18讲练习卷(解析版) 题型:选择题
若i(x+yi)=3+4i,x,y∈R,则复数x+yi的模是( )
A.2 B.3 C.4 D.5
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集15讲练习卷(解析版) 题型:选择题
过椭圆 =1上一点M作圆x2+y2=2的两条切线,点A,B为切点.过A,B的直线l与x轴、y轴分别交于P,Q两点,则△POQ的面积的最小值为( )
=1上一点M作圆x2+y2=2的两条切线,点A,B为切点.过A,B的直线l与x轴、y轴分别交于P,Q两点,则△POQ的面积的最小值为( )
A. B.
B. C.1 D.
C.1 D.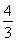
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com