
 ,
, .
.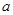 的取值范围,使
的取值范围,使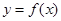 在闭区间
在闭区间 上是单调函数;
上是单调函数; 时,函数
时,函数 的最大值是关于
的最大值是关于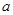 的函数
的函数 .求
.求 ;
;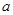 的取值范围,使得对任意的
的取值范围,使得对任意的
 ,恒有
,恒有 成立.
成立. 或
或 ;(2)
;(2)  ;(3)
;(3) .
. .由f(x)在闭区间[-1,3]上是单调函数,能够求出a的取值范围;(2)当a≥0时,m(a)=f(0)=3-a;当-4≤a<0时,m(a)=f(
.由f(x)在闭区间[-1,3]上是单调函数,能够求出a的取值范围;(2)当a≥0时,m(a)=f(0)=3-a;当-4≤a<0时,m(a)=f( )=
)= a2-a+3;当a<-4时,m(a)=f(2)=a+7.分段讨论并比较大小得,能够求出m(a)的最大值及;(3)将
a2-a+3;当a<-4时,m(a)=f(2)=a+7.分段讨论并比较大小得,能够求出m(a)的最大值及;(3)将 在
在
 时恒成立化成
时恒成立化成 在
在
 时恒成立,分类讨论当
时恒成立,分类讨论当 时显然成立,当
时显然成立,当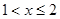 时,
时, 在
在 时恒成立,即可求出a的范围.
时恒成立,即可求出a的范围. 图像的对称轴为
图像的对称轴为 .
. 在闭区间
在闭区间 上是单调函数,所以
上是单调函数,所以 或
或 .
. 或
或 .
. 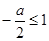 即
即 时
时
 即
即 时
时

 在
在
 时恒成立
时恒成立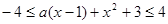 在
在
 时恒成立
时恒成立 在
在
 时恒成立
时恒成立 时显然成立
时显然成立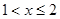 时,
时, 在
在 时恒成立
时恒成立 .
.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:单选题
 ,则f(x)≥﹣2的解集是( )
,则f(x)≥﹣2的解集是( )A.(﹣∞,﹣ ]∪[4,+∞) ]∪[4,+∞) | B.(﹣∞,﹣ ]∪(0,4] ]∪(0,4] |
C.(﹣ ,0]∪[4,+∞) ,0]∪[4,+∞) | D.(﹣ ,0]∪(0,4] ,0]∪(0,4] |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.200只 | B.300只 | C.400只 | D.500只 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 表示不超过
表示不超过 的最大整数,如:
的最大整数,如: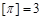 ,
, .给出下列命题:
.给出下列命题: ,都有
,都有 ;
;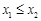 ,则
,则 ;
; ;
; ,则
,则 的值域为
的值域为 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,如果
,如果 ,那么
,那么 是函数
是函数 的极值点;因为函数
的极值点;因为函数 在
在 处的导数值
处的导数值 ,所以
,所以 是函数
是函数 的极值点.”以上推理中( )
的极值点.”以上推理中( )| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.结论正确 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com