
已知函数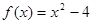 ,设曲线y=f(x)在点
,设曲线y=f(x)在点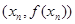 处的切线与x轴的交点为
处的切线与x轴的交点为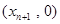 ,(
,(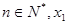 为正数)
为正数)
(1)试用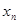 表示
表示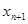
(2)若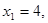 记
记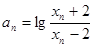 ,证明
,证明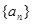 是等比数列,并求数列
是等比数列,并求数列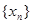 的通项公式;
的通项公式;
(3)若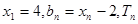 是数列
是数列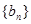 的前n项和,证明:
的前n项和,证明: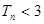
(1)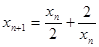 (2)
(2)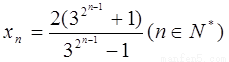 (3)见解析
(3)见解析
【解析】本试题主要是考查了数列与函数,以及不等式的综合运用。
(1)因为曲线y=f(x)在点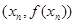 处的切线与x轴的交点为
处的切线与x轴的交点为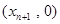 ,利用求出切点的斜率和点到坐标表示切线方程,进而得到结论。
,利用求出切点的斜率和点到坐标表示切线方程,进而得到结论。
(2)由(1)知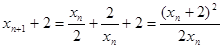 ,
,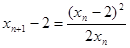
所以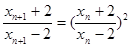 从而得到所证明数列是等比数列。
从而得到所证明数列是等比数列。
(3)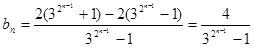 显然
显然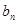 恒大于0 ------------11分
恒大于0 ------------11分
因为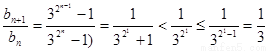
所以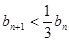
然后分类讨论求和得到证明。
解:(1)因为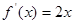 所以曲线y=f(x)在点
所以曲线y=f(x)在点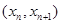 处的切线方程是
处的切线方程是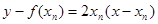 , ---------2分
, ---------2分
令y=0得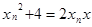
显然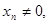 所以
所以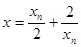
即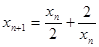 (或
(或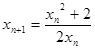 ) ----------4分
) ----------4分
(2)由(1)知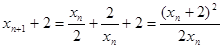 ,
,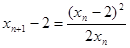
所以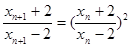 ------------6分
------------6分
从而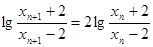 ,即
,即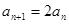 其
其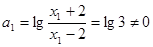
所以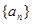 是以
是以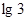 为首项,
为首项,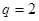 为公比的等比数列 -------8分
为公比的等比数列 -------8分
所以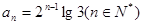 ,即
,即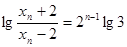
所以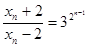 ,所以
,所以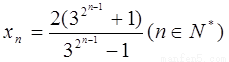 ---------10分
---------10分
(3)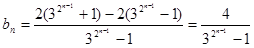 显然
显然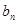 恒大于0 ------11分
恒大于0 ------11分
因为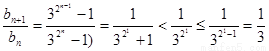
所以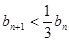 ----------12分
----------12分
当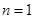 时,显然
时,显然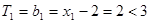
当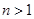 时,
时,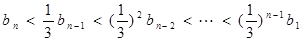
所以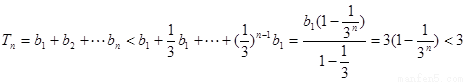
即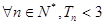 成立,证毕 ------------14分
成立,证毕 ------------14分


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源:2012-2013学年辽宁省本溪一中高三(上)第二次月考数学试卷(理科)(解析版) 题型:解答题
 ,设曲线y=f(x)在与x轴交点处的切线为y=4x-12,f′(x)为f(x)的导函数,且满足f′(2-x)=f′(x).
,设曲线y=f(x)在与x轴交点处的切线为y=4x-12,f′(x)为f(x)的导函数,且满足f′(2-x)=f′(x).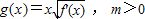 ,求函数g(x)在[0,m]上的最大值;
,求函数g(x)在[0,m]上的最大值;查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁省本溪一中高三(上)第二次月考数学试卷(理科)(解析版) 题型:解答题
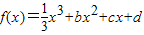 ,设曲线y=f(x)在与x轴交点处的切线为y=4x-12,f′(x)为f(x)的导函数,且满足f′(2-x)=f′(x).
,设曲线y=f(x)在与x轴交点处的切线为y=4x-12,f′(x)为f(x)的导函数,且满足f′(2-x)=f′(x).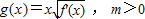 ,求函数g(x)在[0,m]上的最大值;
,求函数g(x)在[0,m]上的最大值;查看答案和解析>>
科目:高中数学 来源:2013年高考数学压轴大题训练:函数的最值问题(解析版) 题型:解答题
 ,设曲线y=f(x)在与x轴交点处的切线为y=4x-12,f′(x)为f(x)的导函数,且满足f′(2-x)=f′(x).
,设曲线y=f(x)在与x轴交点处的切线为y=4x-12,f′(x)为f(x)的导函数,且满足f′(2-x)=f′(x). ,求函数g(x)在[0,m]上的最大值;
,求函数g(x)在[0,m]上的最大值;查看答案和解析>>
科目:高中数学 来源:2012年广东省深圳市高考数学一模试卷(理科)(解析版) 题型:解答题
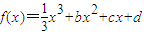 ,设曲线y=f(x)在与x轴交点处的切线为y=4x-12,f′(x)为f(x)的导函数,且满足f′(2-x)=f′(x).
,设曲线y=f(x)在与x轴交点处的切线为y=4x-12,f′(x)为f(x)的导函数,且满足f′(2-x)=f′(x).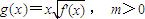 ,求函数g(x)在[0,m]上的最大值;
,求函数g(x)在[0,m]上的最大值;查看答案和解析>>
科目:高中数学 来源:2010年广东省高考冲刺强化训练试卷三文科数学 题型:解答题
(本小题满分14分)已知函数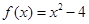 ,设曲线y=f(x)在点(xn,f(xn))处的切线与x轴的交点为(xn+1,0)(n Î N *),x1=4.
,设曲线y=f(x)在点(xn,f(xn))处的切线与x轴的交点为(xn+1,0)(n Î N *),x1=4.
(Ⅰ)用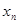 表示xn+1;
表示xn+1;
(Ⅱ)记an=lg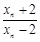 ,证明数列{an}成等比数列,并求数列{xn}的通项公式;
,证明数列{an}成等比数列,并求数列{xn}的通项公式;
(Ⅲ)若bn=xn-2,试比较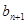 与
与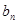 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com