
【题目】已知函数f(x)=(m﹣1)x2+3x﹣2m,(m∈R).
(1)解关于x的不等式f(x)+x2﹣1<4x﹣m;
(2)若f(x)<0的解集为(﹣4,1),g(x)=f(x)﹣x+5,对于n∈N*,证明:![]() .
.
【答案】(1) 当m>0,不等式的解集为(﹣1,1![]() ),当m=0时,不等式的解集为(﹣1,+∞),当
),当m=0时,不等式的解集为(﹣1,+∞),当![]() m<0,不等式的解集为(﹣∞,1
m<0,不等式的解集为(﹣∞,1![]() )∪(﹣1,+∞),当m
)∪(﹣1,+∞),当m![]() 时,不等式的解集为(﹣∞,﹣1)∪(﹣1,+∞),当m
时,不等式的解集为(﹣∞,﹣1)∪(﹣1,+∞),当m![]() ,不等式的解集为(﹣∞,﹣1)∪(1
,不等式的解集为(﹣∞,﹣1)∪(1![]() ,+∞);(2)证明见详解.
,+∞);(2)证明见详解.
【解析】
(1)整理不等式,分解因式,对参数进行分类讨论,即可求得解集;
(2)由不等式的解集求得参数![]() 的值,再利用放缩的方法,证明不等式即可.
的值,再利用放缩的方法,证明不等式即可.
(1)f(x)=(m﹣1)x2+3x﹣2m,
f(x)+x2﹣1<4x﹣m,
∴(m﹣1)x2+3x﹣2m+x2﹣1<4x﹣m,
即mx2﹣x﹣(m+1)<0,
即(x+1)[mx﹣(m+1)]<0,
①当m=0时,﹣x﹣1<0,解得x>﹣1,
②当m>0时,原不等式为(x+1)[x﹣(1![]() )]<0,
)]<0,
解得﹣1<x<1![]() ,
,
③当m<0时,原不等式为(x+1)[x﹣(1![]() )]>0,
)]>0,
令(x+1)[x﹣(1![]() )]=0,
)]=0,
解得x=﹣1或x=1![]() ,
,
⒈若﹣1>1![]() ,即
,即![]() m<0,
m<0,
解得x>﹣1或x<1![]() ,
,
⒉若﹣1=1![]() ,即m
,即m![]() ,
,
解得x≠﹣1,
⒊若﹣1<1![]() ,即m
,即m![]() ,
,
解得x<﹣1或x>1![]() ,
,
综上所述:
当m>0,不等式的解集为(﹣1,1![]() ),
),
当m=0时,不等式的解集为(﹣1,+∞),
当![]() m<0,不等式的解集为(﹣∞,1
m<0,不等式的解集为(﹣∞,1![]() )∪(﹣1,+∞),
)∪(﹣1,+∞),
当m![]() 时,不等式的解集为(﹣∞,﹣1)∪(﹣1,+∞),
时,不等式的解集为(﹣∞,﹣1)∪(﹣1,+∞),
当m![]() ,不等式的解集为(﹣∞,﹣1)∪(1
,不等式的解集为(﹣∞,﹣1)∪(1![]() ,+∞)
,+∞)
(2)∵f(x)<0的解集为(﹣4,1),
∴f(x)=(m﹣1)x2+3x﹣2m=0的两个根为﹣4,1
∴﹣4+1![]() ,﹣4×1
,﹣4×1![]() ,
,
解得m=2,
∴f(x)=x2+3x﹣4,
∴g(x)=f(x)﹣x+5=x2+3x﹣4﹣x+5=x2+2x+1=(x+1)2,
∴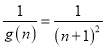 ,
,
要证明![]() ,
,
只要证![]() ,
,
即证 ,
,
①∵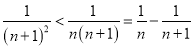 ,
,
∴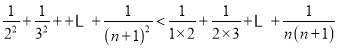
![]() 1
1![]() 1
1![]() ,
,
即证不等式的右边.
②∵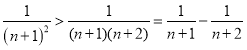 ,
,
∴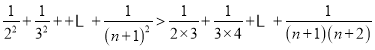
═![]() ,
,
即证不等式的右边.
综上所述:![]() .即证.
.即证.


科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A市某机构为了调查该市市民对我国申办2034年足球世界杯的态度,随机选取了140位市民进行调查,调查结果统计如下:
支持 | 不支持 | 合计 | |
男性市民 | 60 | ||
女性市民 | 50 | ||
合计 | 70 | 140 |
(1)根据已知数据,把表格数据填写完整;
(2)若在被调查的支持申办足球世界杯的男性市民中有5位退休老人,其中2位是教师,求从这5人中随机抽取3人至多有1人是教师的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学为调研学生在![]() ,
, ![]() 两家餐厅用餐的满意度,从在
两家餐厅用餐的满意度,从在![]() ,
, ![]() 两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.
两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.
整理评分数据,将分数以10为组距分成6组: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,得到
,得到![]() 餐厅分数的频率分布直方图,和
餐厅分数的频率分布直方图,和![]() 餐厅分数的频数分布表:
餐厅分数的频数分布表:
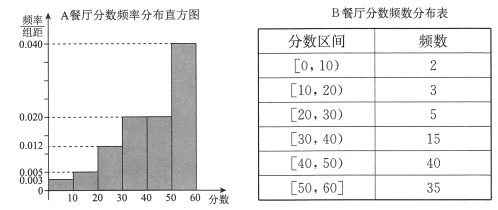
(Ⅰ)在抽样的100人中,求对![]() 餐厅评分低于30的人数;
餐厅评分低于30的人数;
(Ⅱ)从对![]() 餐厅评分在
餐厅评分在![]() 范围内的人中随机选出2人,求2人中恰有1人评分在
范围内的人中随机选出2人,求2人中恰有1人评分在![]() 范围内的概率;
范围内的概率;
(Ⅲ)如果从![]() ,
, ![]() 两家餐厅中选择一家用餐,你会选择哪一家?说明理由.
两家餐厅中选择一家用餐,你会选择哪一家?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有2位男生,3位女生去参加一个联欢活动,该活动有甲、乙两个项目可供参加者选择.
(Ⅰ)为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个项目联欢,掷出点数为1或2的人去参加甲项目联欢,掷出点数大于2的人去参加乙项目联欢.求这5人中恰好有3人去参加甲项目联欢的概率;
(Ⅱ)若从这5人中随机选派3人去参加甲项目联欢,设![]() 表示这3个人中女生的人数,求随机变量
表示这3个人中女生的人数,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且acosC+ccosA=2bcosA.
(1)求角A的值;
(2)若![]() ,
, ![]() ,求△ABC的面积S.
,求△ABC的面积S.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产![]() 、
、![]() 两种产品,生产每
两种产品,生产每![]() 产品所需的劳动力和煤、电消耗如下表:
产品所需的劳动力和煤、电消耗如下表:
产品品种 | 劳动力(个) | 煤 | 电 |
|
|
|
|
|
|
|
|
已知生产![]() 产品的利润是
产品的利润是![]() 万元,生产
万元,生产![]() 产品的利润是
产品的利润是![]() 万元.现因条件限制,企业仅有劳动力
万元.现因条件限制,企业仅有劳动力![]() 个,煤
个,煤![]() ,并且供电局只能供电
,并且供电局只能供电![]() ,则企业生产
,则企业生产![]() 、
、![]() 两种产品各多少吨,才能获得最大利润?
两种产品各多少吨,才能获得最大利润?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com