
【题目】已知函数f(x)= ![]() .
.
(1)证明f(x)为偶函数;
(2)若不等式k≤xf(x)+ ![]() 在x∈[1,3]上恒成立,求实数k的取值范围;
在x∈[1,3]上恒成立,求实数k的取值范围;
(3)当x∈[ ![]() ,
, ![]() ](m>0,n>0)时,函数g(x)=tf(x)+1,(t≥0)的值域为[2﹣3m,2﹣3n],求实数t的取值范围.
](m>0,n>0)时,函数g(x)=tf(x)+1,(t≥0)的值域为[2﹣3m,2﹣3n],求实数t的取值范围.
【答案】
(1)证明:函数的定义域为(﹣∞,0)∪(0,+∞)关于原点对称,
∵f(﹣x)= ![]() =f(x),
=f(x),
∴f(x)为偶函数
(2)k≤xf(x)+ ![]() =x在x∈[1,3]上恒成立,
=x在x∈[1,3]上恒成立,
∴k≤1
(3)g(x)=tf(x)+1=t(1﹣ ![]() )+1 (t≥0)在x∈[
)+1 (t≥0)在x∈[ ![]() ,
, ![]() ]上递增,
]上递增,
∴g( ![]() )=2﹣3m,g(
)=2﹣3m,g( ![]() )=2﹣3n,
)=2﹣3n,
∴t(1﹣m2)+1=2﹣3m,t(1﹣n2)+1=2﹣3n,
∴m,n是t(1﹣x2)+1=2﹣3x的两个不相等的正跟,
∴tx2﹣3x+1﹣t=0(t>0),
∴△=9﹣4t(1﹣t)>0,
![]() >0,
>0,
![]() >0,
>0,
∴0<t<1
【解析】(1)利用定义判断函数的奇偶性,先求定义域,再判断f(﹣x)= ![]() =f(x);(2)直接求右表达式的最小值即可;(3)得出g(x)=tf(x)+1=t(1﹣
=f(x);(2)直接求右表达式的最小值即可;(3)得出g(x)=tf(x)+1=t(1﹣ ![]() )+1 (t≥0)在x∈[
)+1 (t≥0)在x∈[ ![]() ,
, ![]() ]上递增,可得出g(
]上递增,可得出g( ![]() )=2﹣3m,g(
)=2﹣3m,g( ![]() )=2﹣3n,
)=2﹣3n,
构造一方程m,n是t(1﹣x2)=2﹣3x的两个不相等的正跟,利用二次函数和韦达定理得出t的范围.
【考点精析】根据题目的已知条件,利用函数奇偶性的性质的相关知识可以得到问题的答案,需要掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图1,在![]() △
△![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 分别为边
分别为边![]() 的中点,点
的中点,点![]() 分别为线段
分别为线段![]() 的中点.将△
的中点.将△![]() 沿
沿![]() 折起到△
折起到△![]() 的位置,使
的位置,使![]() .点
.点![]() 为线段
为线段![]() 上的一点,如图2.
上的一点,如图2.
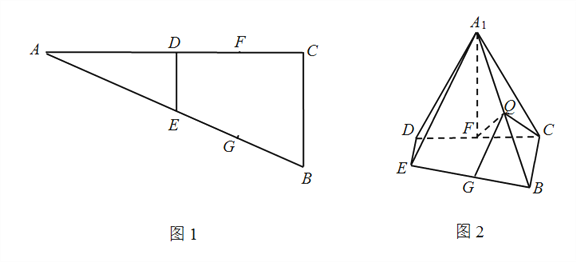
(Ⅰ)求证: ![]() ;
;
(Ⅱ)线段![]() 上是否存在点
上是否存在点![]() 使得
使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的长,若不存在,请说明理由;
的长,若不存在,请说明理由;
(Ⅲ)当![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论中正确的序号是 .
①函数y=ax(a>0且a≠1)与函数 ![]() (a>0且a≠1)的定义域相同;
(a>0且a≠1)的定义域相同;
②函数y=k3x(k>0)(k为常数)的图象可由函数y=3x的图象经过平移得到;
③函数 ![]() (x≠0)是奇函数且函数
(x≠0)是奇函数且函数 ![]() (x≠0)是偶函数;
(x≠0)是偶函数;
④若x1是函数f(x)的零点,且m<x1<n,则f(m)f(n)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)= ![]() ,x∈(﹣2,2)
,x∈(﹣2,2)
(1)判断f(x)的奇偶性并说明理由;
(2)求证:函数f(x)在(﹣2,2)上是增函数;
(3)若f(2+a)+f(1﹣2a)>0,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集为实数集R,A={x|3≤x<7},B={x| ![]() ≤2x≤8},C={x|x<a}.
≤2x≤8},C={x|x<a}.
(1)求R(A∪B)
(2)如果A∩C≠,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位小学生各有2008年奥运吉祥物“福娃”5个(其中“贝贝”、“晶晶”、“欢欢”、“迎迎”和“妮妮各一个”),现以投掷一个骰子的方式进行游戏,规则如下:当出现向上的点数是奇数时,甲赢得乙一个福娃;否则乙赢得甲一个福娃,规定掷骰子的次数达9次时,或在此前某人已赢得所有福娃时游戏终止.记游戏终止时投掷骰子的次数为ξ
(1)求掷骰子的次数为7的概率;
(2)求ξ的分布列及数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选修4-4:坐标系与参数方程】
在直角坐标系![]() 中圆C的参数方程为
中圆C的参数方程为![]() (
(![]() 为参数),以原点O为极点,
为参数),以原点O为极点, ![]() 轴的非负半轴为极轴建立极坐标系,直线
轴的非负半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求圆C的直角坐标方程及其圆心C的直角坐标;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com