【题目】(1)求与双曲线
有相同的焦点且过点
的双曲线标准方程；
(2)求焦点在直线
上的抛物线的标准方程.
【答案】(1) 
(2)
或
【解析】
(1)先求出双曲线的c,再代点P的坐标即得a,b的方程组，解方程组即得双曲线的标准方程.(2)
先根据焦点在直线x﹣2y+2=0上求得焦点的坐标，再分抛物线以x轴对称式和y轴对称式，
分别设出抛物线的标准方程，求得p，即可得到抛物线的方程．
由题得
设双曲线的标准方程为
，
代点P的坐标得
解方程组
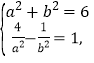得
.
(2) ∵焦点在直线x﹣2y+2=0上，且抛物线的顶点在原点，对称轴是坐标轴，
焦点的坐标为A（0， 1），或（-2，0），
若抛物线以y轴对称式，设方程为x2=2py，
=1，求得p=2，∴此抛物线方程为x2=4y；
若抛物线以x轴对称式，设方程为y2=-2px，=2，求得p=4，∴此抛物线方程为y2=-8x；
故所求的抛物线的方程为或.
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
周周清检测系列答案科目：高中数学 来源： 题型：
【题目】已知函数f（x）= 
，曲线f（x）= 在点（e，f（e））处的切线与直线e2x﹣y+e=0垂直．（注：e为自然对数的底数） （Ⅰ）若函数f（x）在区间（m，m+1）上存在极值，求实数m的取值范围；
（Ⅱ）求证：当x＞1时， 
＞ 
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设集合A={x|﹣1≤x≤2}，B={x|x2﹣x+（m﹣m2）＜0}．
（1）当m＜ 
时，化简集合B；
（2）p：x∈A，命题q：x∈B，且命题p是命题q的必要不充分条件，求实数m的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，AB是的⊙O直径，CB与⊙O相切于B，E为线段CB上一点，连接AC、AE分别交⊙O于D、G两点，连接DG交CB于点F． 
（1）求证：C、D、G、E四点共圆．
（2）若F为EB的三等分点且靠近E，EG=1，GA=3，求线段CE的长．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（本小题满分1６分）平面直角坐标系xoy中，直线
截以原点O为圆心的圆所得的弦长为
（1）求圆O的方程；
（2）若直线
与圆O切于第一象限，且与坐标轴交于D，E，当DE长最小时，求直线的方程；
（3）设M，P是圆O上任意两点，点M关于ｘ轴的对称点为N，若直线MP、NP分别交于ｘ轴于点（ｍ，０）和（ｎ，０），问ｍｎ是否为定值？若是，请求出该定值；若不是，请说明理由。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在△ABC中，角A、B、C所对的边分别为a、b、c，| 
|=5，20a 
+15b 
+12c = 
， 
=2 
，则 
的值为（ ）
A.
B.﹣ 
C.﹣
D.﹣8
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列{an}的各项均为正数，满足a1=1，ak+1﹣ak=ai ． （i≤k，k=1，2，3，…，n﹣1）
（1）求证： 
；
（2）若{an}是等比数列，求数列{an}的通项公式；
（3）设数列{an}的前n项和为Sn ， 求证： 
．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
