练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    过抛物线x2＝4y上不同两点A、B分别作抛物线的切线相交于P点，(1)求点P的轨迹方程；

    (2)已知点F(0，1)，是否存在实数λ使得？若存在，求出λ的值，若不存在，请说明理由．

    答案：
    解析：

    　　解法(一)：(1)设

    　　由得：，

    　　　　4分

    　　直线PA的方程是：即①

    　　同理，直线PB的方程是：②　　6分

    　　由①②得：

    　　∴点P的轨迹方程是　　8分

    　　(2)由(1)得：

    　　，

    　　，所以

    　　故存在＝1使得　　14分

    　　解法(二)：(1)∵直线PA、PB与抛物线相切，且

    　　∴直线PA、PB的斜率均存在且不为0，且

    　　设PA的直线方程是

    　　由得：　　4分

    　　即

    　　即直线PA的方程是：

    　　同理可得直线PB的方程是：　　6分

    　　由得：

    　　故点P的轨迹方程是　　8分

    　　(2)由(1)得：

    　　，

    　　

    　　

    　　故存在＝1使得　　14分


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：江苏省丹阳高级中学2007年高三数学月考试卷及答案 题型：044

    过抛物线x2＝4y上不同两点A、B分别作抛物线的切线相交于P点，(1)求点P的轨迹方程；(2)已知点F(0，1)，是否存在实数λ使得？若存在，求出λ的值，若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：增城市2007届华侨中学高三四月份月考试题\数学(理科) 题型：044

    已知过抛物线x2＝4y的对称轴上一点P(0，m)(m＞0)作直线l，l与抛物线交于A、B两点．

    (1)若角∠AOB为锐角(O为坐标原点)，求实数m的取值范围；

    (2)若l的方程为x－2y＋12＝0，且过A、B两点的圆C与抛物线在点且(A在第一象限)处有共同的切线，求圆C的方程．

    查看答案和解析>>

    科目：高中数学 来源：101网校同步练习　高二数学　苏教版(新课标·2004年初审) 苏教版 题型：044

    如图，对每个正整数n，An(xn，yn)是抛物线x2＝4y上的点，过焦点F的直线FAn交抛物线于另一点Bn(Sn，tn)．Cn为抛物线上分别以An与Bn为切点的两条切线的交点．

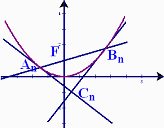
    (1)求证∠AnCnBn＝90o；

    (2)求证点Cn的纵坐标是一个定值，并求这个定值；

    (3)若|FC1|、|FC2|、|FC3|、…、|FCn|构成首项为3，公比为2的等比数列，求|A1B1|＋|A2B2|＋|A3B3|＋…＋|AnBn|．

    查看答案和解析>>

    科目：高中数学 来源：广州市2008届高中教材变式题9：圆锥曲线与方程 题型：047

    如图，对每个正整数n，An(xn，yn)是抛物线x2＝4y上的点，过焦点F的直线FAn交抛物线于另一点Bn(sn，tn)．

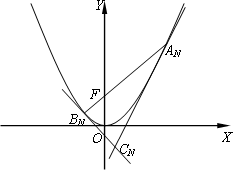
    (Ⅰ)试证：xnsn＝－4(n≥1)；

    (Ⅱ)取xn＝2n，并记Cn为抛物线上分别以An与Bn为切点的两条切线的交点．试证：|FC1|＋|FC2|＋…＋|FCn|＝2n－2－n+1＋1．

    查看答案和解析>>

    同步练习册答案