
【题目】如图,在多面体![]() 中,
中,![]() 平面
平面![]() ,且
,且![]() 是边长为2的等边三角形,
是边长为2的等边三角形,![]() .
.

(1)若![]() 是线段
是线段![]() 的中点,证明:直线
的中点,证明:直线![]() 面
面![]() ;
;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:取BC的中点G,连接AG、FG,利用![]() 为三角形
为三角形![]() 的中位线,
的中位线,![]() ,
,![]() ,说明四边形
,说明四边形![]() 是平行四边形,因此
是平行四边形,因此![]() ,问题转化为证明
,问题转化为证明![]() 平面
平面![]() ,证明线面垂直,只需寻求线线垂直,因三角形ABC为等边三角形,则
,证明线面垂直,只需寻求线线垂直,因三角形ABC为等边三角形,则![]() ,又DB⊥平面ABC,则
,又DB⊥平面ABC,则![]() ,问题得以解决,第二步首先找出二面角,连接
,问题得以解决,第二步首先找出二面角,连接![]() ,过
,过![]() 在面
在面![]() 内作
内作![]() 的垂线,垂足为
的垂线,垂足为![]() 连接
连接![]() .因为
.因为![]() ,
,![]() ,在三角形DBC中,
,在三角形DBC中,![]() ,
,![]() ,
,![]() 所以易证得
所以易证得![]() 为二面角D-EC-B的平面角,在直角三角形
为二面角D-EC-B的平面角,在直角三角形![]() 中,求出
中,求出![]() 的余弦;
的余弦;
试题解析:(ⅰ)证明:取![]() 的中点
的中点![]() ,连接
,连接![]()
![]()
![]()
![]() 又因为
又因为![]()
![]() 为平行四边形,
为平行四边形,![]()
![]() .
.
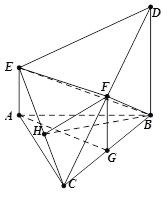
(ⅱ)连接![]() ,过
,过![]() 在面
在面![]() 内作
内作![]() 的垂线,垂足为
的垂线,垂足为![]() ,连接
,连接![]() .因为
.因为![]() ,
,![]()
又![]()
![]() ,
,![]() 所以易证得
所以易证得![]() 为二面角D-EC-B的平面角;
为二面角D-EC-B的平面角;
在![]() 中,
中,![]()
![]() 所以易求得
所以易求得![]() ,在直角
,在直角![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,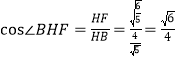 ,
,
所以二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]()


 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源: 题型:
【题目】为了解七班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
喜爱打篮球 | 不喜爱打篮球 | 合 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为![]() .
.
(1)请将上面的列联表补充完整(不用写计算过程);
(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理由;
(3)现从女生中抽取2人进一步调查,设其中喜爱打篮球的女生人数为![]() ,求
,求![]() 的分布列与期望.
的分布列与期望.
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05[ | 0.025 | 0.01 | 0.005 | 0.001 |
| 2.072 | 2.70 | 3.841 | 5.024 | 6.635 | 7.879 | 10.82 |
(参考公式: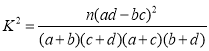 ,其中
,其中![]() )
)![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为评估设备![]() 生产某种零件的性能,从设备
生产某种零件的性能,从设备![]() 生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
直径 | 58 | 59 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合计 |
件数 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
经计算,样本的平均值![]() ,标准差
,标准差![]() ,以频率值作为概率的估计值,用样本估计总体.
,以频率值作为概率的估计值,用样本估计总体.
(1)将直径小于等于![]() 或直径大于
或直径大于![]() 的零件认为是次品,从设备
的零件认为是次品,从设备![]() 的生产流水线上随意抽取3个零件,计算其中次品个数
的生产流水线上随意抽取3个零件,计算其中次品个数![]() 的数学期望
的数学期望![]() ;
;
(2)为评判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为![]() ,并根据以下不等式进行评判(
,并根据以下不等式进行评判(![]() 表示相应事件的概率):①
表示相应事件的概率):①![]() ;②
;②![]() ;③
;③![]() .评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁,试判断设备
.评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁,试判断设备![]() 的性能等级并说明理由.
的性能等级并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖南)如下图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E、F分别是BC、CC1的中点.
(1)证明:平面AEF⊥平面B1BCC1;
(2)若直线A1C与平面A1ABB1所成的角为45°,求三棱锥F-AEC的体积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,x∈R.
,x∈R.
(1)判断函数的奇偶性,并说明理由;
(2)利用函数单调性定义证明:![]() 在
在![]() 上是增函数;
上是增函数;
(3)若![]() 对任意的x∈R,任意的
对任意的x∈R,任意的![]() 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]() ,直线
,直线![]() :
:![]() (
(![]() 为参数,
为参数,![]() ).
).
(Ⅰ)求直线![]() 的普通方程;
的普通方程;
(Ⅱ)在曲线![]() 上求一点
上求一点![]() ,使它到直线
,使它到直线![]() 的距离最短,并求出点
的距离最短,并求出点![]() 的极坐标.
的极坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com