
已知与圆C:x2+y2-2x-2y+1=0相切的直线l交x轴,y轴于A,B两点,
OA|=a,|OB|=b(a>2,b>2).
(Ⅰ)求证:(a-2)(b-2)=2;
(Ⅱ)求线段AB中点的轨迹方程;
(Ⅲ)求△AOB面积的最小值.
(Ⅰ)见解析 (Ⅱ) (x-1)(y-1)=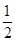 (x>1,y>1) (Ⅲ) 3+2
(x>1,y>1) (Ⅲ) 3+2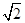
【解析】本题考查的知识点是直线和圆的方程的应用,轨迹方程,直线与圆的位置关系,考查的解题方法为坐标法,难度中等.
(1)由已知中圆C:x2+y2-2x-2y+1=0,直线交x轴、y轴于A、B两点|OA|=a,|OB|=b,我们设以分别求出直线的一般方程,和圆的标准方程,然后根据直线与圆相切,圆心到直线的距离等于半径得到结论;
(2)设线段AB的中点M(x,y),代入(1)的结论,整理后,即可得到答案;
(3)S△AOB=
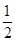 |ab|,结合(1)的结论,及均值不等式,即可得到答案.
|ab|,结合(1)的结论,及均值不等式,即可得到答案.
(Ⅰ)证明:圆的标准方程是(x-1)2+(y-1)2=1,设直线方程为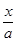 +
+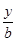 =1,即bx+ay-ab=0,圆心到该直线的距离d=
=1,即bx+ay-ab=0,圆心到该直线的距离d=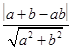 =1,………………………2分
=1,………………………2分
即a2+b2+a2b2+2ab-2a2b-2ab2=a2+b2,即a2b2+2ab-2a2b-2ab2=0,即ab+2-2a-2b=0,即(a-2)(b-2)=2.……………………………4分
(Ⅱ)设AB中点M(x,y),则a=2x,b=2y,代入(a-2)(b-2)=2,得(x-1)(y-1)=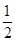 (x>1,y>1).……………………………………………………………8分
(x>1,y>1).……………………………………………………………8分
(Ⅲ)由(a-2)(b-2)=2得ab+2=2(a+b)≥4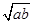 ,解得
,解得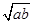 ≥2+
≥2+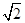 (舍去
(舍去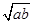 ≤2-
≤2-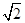 ),………………………………………………………………………10分
),………………………………………………………………………10分
当且仅当a=b时,ab取最小值6+4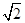 ,所以△AOB面积的最小值是3+2
,所以△AOB面积的最小值是3+2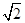 .…12分
.…12分


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:
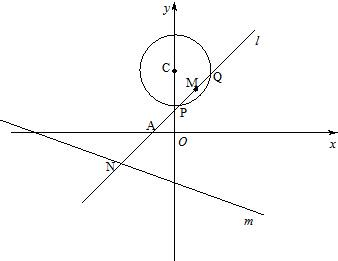 如图,已知定圆C:x2+(y-3)2=4,定直线m:x+3y+6=0,过A(-1,0)的一条动直线l与直线相交于N,与圆C相交于P,Q两点,M是PQ中点.
如图,已知定圆C:x2+(y-3)2=4,定直线m:x+3y+6=0,过A(-1,0)的一条动直线l与直线相交于N,与圆C相交于P,Q两点,M是PQ中点.| 3 |
| AM |
| AN |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com