
【题目】已知函数![]() (a为常数)的最大值为0.
(a为常数)的最大值为0.
(1)求实数a的值;
(2)设函数![]() ,当
,当![]() 时,求证:函数
时,求证:函数![]() 有两个不同的零点
有两个不同的零点![]() ,
,![]() (
(![]() ),且
),且![]() .
.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程为![]() (1+cos2θ)=8sinθ.
(1+cos2θ)=8sinθ.
(1)求曲线C的普通方程;
(2)直线l的参数方程为![]() ,t为参数直线
,t为参数直线![]() 与y轴交于点F与曲线C的交点为A,B,当|FA||FB|取最小值时,求直线
与y轴交于点F与曲线C的交点为A,B,当|FA||FB|取最小值时,求直线![]() 的直角坐标方程.
的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两个商场同时出售一款西门子冰箱,其中甲商场位于老城区中心,乙商场位于高新区.为了调查购买者的年龄与购买冰箱的商场选择是否具有相关性,研究人员随机抽取了1000名购买此款冰箱的用户作调研,所得结果如表所示:
50岁以上 | 50岁以下 | |
选择甲商场 | 400 | 250 |
选择乙商场 | 100 | 250 |
(1)判断是否有![]() 的把握认为购买者的年龄与购买冰箱的商场选择具有相关性;
的把握认为购买者的年龄与购买冰箱的商场选择具有相关性;
(2)由于乙商场的销售情况未达到预期标准,商场决定给冰箱的购买者开展返利活动具体方案如下:当天卖出的前60台(含60台)冰箱,每台商家返利200元,卖出60台以上,超出60台的部分,每台返利50元.现将返利活动开展后15天内商场冰箱的销售情况统计如图所示:与此同时,老张得知甲商场也在开展返利活动,其日返利额的平均值为11000元,若老张将选择返利较高的商场购买冰箱,请问老张应当去哪个商场购买冰箱

附: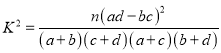 ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线![]() 的焦点为F且斜率为k的直线l交曲线C于
的焦点为F且斜率为k的直线l交曲线C于![]() 、
、![]() 两点,交圆
两点,交圆![]() 于M,N两点(A,M两点相邻).
于M,N两点(A,M两点相邻).
(1)求证:![]() 为定值;
为定值;
(2)过A,B两点分别作曲线C的切线![]() ,
,![]() ,两切线交于点P,求
,两切线交于点P,求![]() 与
与![]() 面积之积的最小值.
面积之积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于圆周率![]() ,数学发展史上出现过许多有创意的求法,如著名的普丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计
,数学发展史上出现过许多有创意的求法,如著名的普丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计![]() 的值:先请120名同学每人随机写下一个x,y都小于1的正实数对
的值:先请120名同学每人随机写下一个x,y都小于1的正实数对![]() ,再统计其中x,y能与1构成钝角三角形三边的数对
,再统计其中x,y能与1构成钝角三角形三边的数对![]() 的个数m,最后根据统计个数m估计
的个数m,最后根据统计个数m估计![]() 的值.如果统计结果是
的值.如果统计结果是![]() ,那么可以估计
,那么可以估计![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
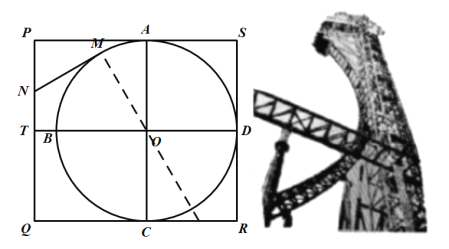
【题目】某游乐场过山车轨道在同一竖直钢架平面内,如图所示,矩形![]() 的长
的长![]() 为130米,宽
为130米,宽![]() 为120米,圆弧形轨道所在圆的圆心为0,圆O与
为120米,圆弧形轨道所在圆的圆心为0,圆O与![]() ,
,![]() ,
,![]() 分别相切于点A,D,CT为
分别相切于点A,D,CT为![]() 的中点.现欲设计过山车轨道,轨道由五段连接而成:出发点N在线段
的中点.现欲设计过山车轨道,轨道由五段连接而成:出发点N在线段![]() 上(不含端点,游客从点Q处乘升降电梯至点N),轨道第一段
上(不含端点,游客从点Q处乘升降电梯至点N),轨道第一段![]() 与圆O相切于点M,再沿着圆孤轨道
与圆O相切于点M,再沿着圆孤轨道![]() 到达最高点A,然后在点A处沿垂直轨道急速下降至点O处,接着沿直线轨道
到达最高点A,然后在点A处沿垂直轨道急速下降至点O处,接着沿直线轨道![]() 滑行至地面点G处(设计要求M,O,G三点共线),最后通过制动装置减速沿水平轨道
滑行至地面点G处(设计要求M,O,G三点共线),最后通过制动装置减速沿水平轨道![]() 滑行到达终点R记
滑行到达终点R记![]() 为
为![]() ,轨道总长度为l米.
,轨道总长度为l米.
(1)试将l表示为![]() 的函数
的函数![]() ,并写出
,并写出![]() 的取值范围;
的取值范围;
(2)求l最小时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|2x﹣3|+|x+2|
(1)求不等式f(x)≤5的解集;
(2)若关于x的不等式f(x)≤a﹣|x|在区间[﹣1,2]上恒成立,求实数a的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com